P5385 [Cnoi2019] Momentary Illusion Realm.

There used to be a sad and touching story here, but the problem setter deleted the file and it was lost.

Initially, you are given an undirected graph $G$ with $n$ vertices and $m$ edges. The vertices are numbered $1,2,\cdots,n$. Now, number all $m$ edges in $G$ in order and arrange them into an edge sequence of length $m$: $E=(e_1,e_2,\cdots,e_m)$, where $e_i=(u_i,v_i)$ is an ordered pair representing an undirected edge connecting $u_i$ and $v_i$. Then Cirno will give you $q$ query pairs $(l,r)$, asking: “If we only keep the edges $e_l,e_{l+1},\cdots,e_r$ in this interval, what is the number of connected components in the graph?” Time is tight. You need to design an algorithm as fast as possible to answer Cirno’s queries. Also, since in some cases queries may depend on each other, your program must run online.

The first line contains four integers separated by spaces: $n$, $m$, $q$, $t$, where $t$ is the forced-online parameter used to decrypt the real queries. The next $m$ lines describe the edges. The $i$-th line contains two integers $u_i$ and $v_i$ separated by a space, representing the edge sequence $E$. The next $q$ lines each contain two integers $l', r'$ separated by spaces, representing an encrypted query. The real query pair $(l,r)$ is decrypted as follows. ```plain-text DecodeQuery( l', r', m, t, last_ans ) (l, r) 0 THEN l

Output $q$ lines, each being the answer to one query.

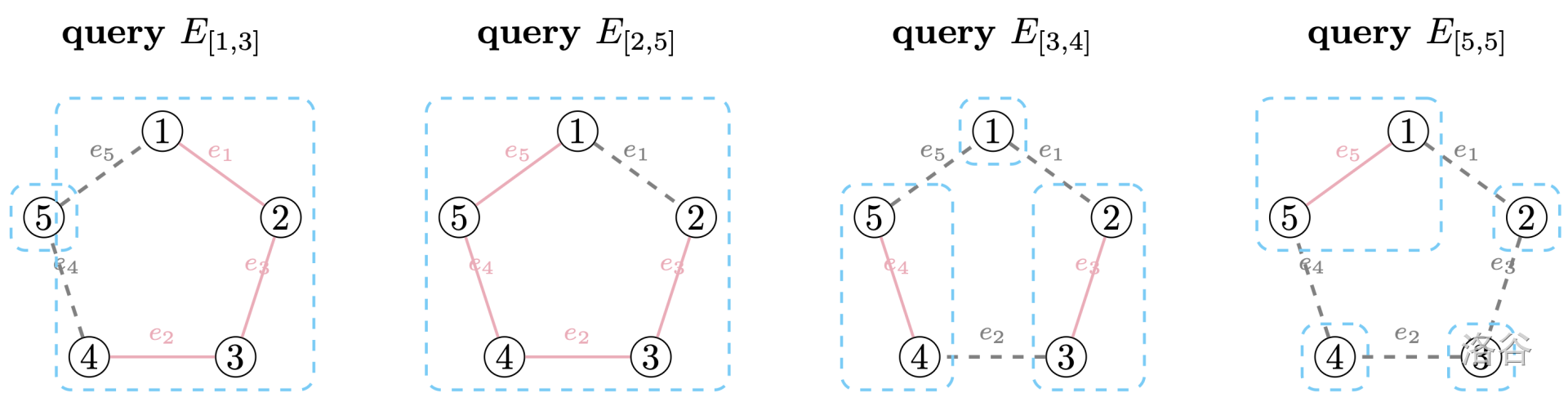
**Sample Explanation**  **Constraints and Notes** For $100\%$ of the testdata, it is guaranteed that $1\le |V| \le 10^5$, $1\le |E| \le 2\times 10^5$, $1\le q \le 10^5$, and $t \in \{0,1\}$. **Note that the testdata may contain multiple edges and self-loops**. **Subtasks** Subtask 1 ($15$ points): $|V|, |E|, q \le 5000$. Subtask 2 ($25$ points): $t = 0$. Subtask 3 ($20$ points): $|V| \le 10^4$, $|E|, q \le 3\times 10^4$. Subtask 4 ($40$ points): No special restrictions. Translated by ChatGPT 5