P5392 [Cnoi2019] Appointment of the Cedar Tree

Because Cirno suddenly became lazy, the background story is skipped.

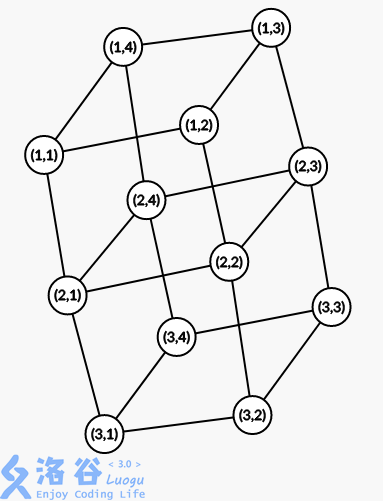
Cirno defines a type of graph: the cylindrical network $G(L, x)$. $G(L, x)$ denotes a graph with $L \times x$ nodes. Each node is represented by an ordered pair of integers $(a, b)$, where $(1 \le a \le L, 1 \le b \le x)$. For $\forall i \in (1, L],\ j \in (0, x]$, there is an edge between node $(i, j)$ and node $(i - 1, j)$. For $\forall i \in [1, L],\ j \in (0, x)$, there is an edge between node $(i, j)$ and node $(i, j + 1)$. For $\forall i \in [1, L]$, there is an edge between node $(i, x)$ and node $(i, 1)$. Now Cirno wants to know the number of **independent sets** of $G(L, x)$. Since you cannot do big integer arithmetic, you need to output the answer modulo $998244353$.

One line with two integers $L$ and $x$.

One line with one integer, the number of independent sets of $G(L, x)$ modulo $998244353$.

For the first $10\%$ of the testdata, $L, x \le 8$. For the first $30\%$ of the testdata, $x \le 8$. For the first $50\%$ of the testdata, $x \le 11$. For $100\%$ of the testdata, $0 < L \le 10^{18},\ 0 < x \le 17$. This problem uses bundled tests. The figure below is an example of $G(3, 4)$.  Translated by ChatGPT 5