P5441 [XR-2] Scars.

> At the end of a long day, I come before you. You will see my scars. You will know that I was once hurt, and that I have also healed. — Tagore, *Love This City Deeply*.

Country X has suffered an unprecedented earthquake. People are covered in scars, and the whole country is shattered. To help people heal, and also to allow Country X to survive, the King of Country X decides to rebuild the country. The King decides to first build $n$ cities. Since the King likes odd numbers, $n$ is odd. After the cities are built, a road must be built between every pair of cities, i.e., a total of $\frac{n(n-1)}{2}$ roads. However, the cost of building bidirectional roads is too high. After building $n$ cities, the remaining budget is enough to build at most $n$ bidirectional roads, and all other roads can only be built as one-way roads. Fortunately, the direction does not affect the cost of building a one-way road, so the directions of all one-way roads can be chosen arbitrarily. In addition, after the rebuilding is completed, the King will designate $4$ cities as the core cities of Country X. To promote the development of Country X, for any two of these $4$ core cities, they must be able to reach each other without passing through non-core cities. The King hopes that you can provide him with a road construction plan such that, after the rebuilding is completed, the number of ways to choose $4$ core cities is maximized.

One line containing a positive integer $n(1 \le n \le 99)$, guaranteed that $n$ is odd, meaning there are $n$ cities.

The first line contains an integer, representing the maximum number of ways to choose $4$ core cities. The next $n$ lines each contain $n$ positive integers describing an adjacency matrix, representing your road construction plan. Specifically, the $j$-th number in the $i$-th line is $1$ if city $i$ can reach city $j$ via a road, and $0$ if city $i$ cannot reach city $j$ via a road. We explain in detail in $3$ cases: 1. If the road between $i$ and $j$ is a one-way road from $i$ to $j$, then the number in row $i$, column $j$ of the adjacency matrix is $1$, and the number in row $j$, column $i$ is $0$. 2. If the road between $i$ and $j$ is a bidirectional road, then both the number in row $i$, column $j$ and the number in row $j$, column $i$ are $1$. You must ensure that at most $n$ bidirectional roads are built. 3. If $i = j$, then the number in row $i$, column $j$ (the number in row $j$, column $i$) is $0$.

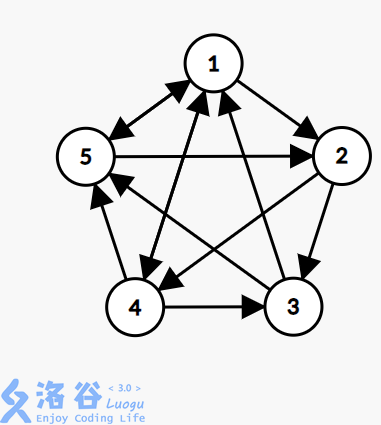
[Sample $1$ Explanation] Since there are only $3$ points in total, the number of ways to choose $4$ core cities must be $0$. So you only need to ensure that the construction plan satisfies the requirements. [Sample $2$ Explanation]  Obviously, among $5$ points, choosing any $4$ points satisfies the core-city condition, so the maximum number of ways is $5$. [Constraints] This problem has $50$ test points, each worth $2$ points. For the $i$-th test point, $n = 2i - 1$. For each test point, there are five possible outcomes: 1. Output format error, including: not outputting the maximum number of ways, not outputting the adjacency matrix, outputting extra information, etc. You will not get any points for this test point, and we cannot determine the return result of the Special Judge. 2. The maximum number of ways is not computed correctly, even if the constructed road plan is correct. You will get $0\%$ of the score for this test point (i.e., $0$ points). The Special Judge will return WA and output “The answer is wrong.” 3. The maximum number of ways is computed correctly, but the constructed road plan does not satisfy the requirements, including: numbers in the adjacency matrix that are not $0$ or $1$, self-loops, a pair of cities with no road between them, more than $n$ bidirectional roads, etc. You will get $50\%$ of the score for this test point (i.e., $1$ point). The Special Judge will return WA and output “The answer is correct, but your plan breaks the rules.” 4. The maximum number of ways is computed correctly, and the constructed road plan satisfies the requirements, but the number of ways to choose $4$ core cities is not maximized. You will get $50\%$ of the score for this test point (i.e., $1$ point). The Special Judge will return WA and output “The answer is correct, but your plan is wrong.” 5. The maximum number of ways is computed correctly, and the road construction plan is also constructed correctly. You will get $100\%$ of the score for this test point (i.e., $2$ points). The Special Judge will return AC and output “The answer is correct.” Translated by ChatGPT 5