P5448 [THUPC 2018] Good Graph Counting

This problem is very simple. It does not even have a background story. But to help you understand the problem smoothly, the kind Yazid will introduce some concepts. * Simple graph: a graph with no multiple edges and no self-loops. (A multiple edge means two completely identical edges, and a self-loop means an edge whose two endpoints are the same vertex.) * Complement graph: the complement of a graph $G$ has exactly the same vertices as $G$, and there is an edge between any two vertices if and only if they are not adjacent in $G$.

We define an undirected simple graph to be **good** as follows: 1. A single vertex is good. 2. A graph formed by taking several good graphs as connected components is good. 3. The complement of a good graph is good. Given a positive integer $n$. Find, modulo the prime $P$, the number of essentially different good graphs on $n$ vertices. (Here $P$ is a constant; see **Input Format** for details.) Two good graphs are considered **essentially different** if and only if, no matter how you relabel one graph, it still cannot become exactly the same as the other graph.

The input contains multiple test cases. The first line contains two integers $T, P$ separated by spaces, representing the number of test cases and the modulus. Then each test case is described as follows: * One line with one integer $n$, meaning the number of vertices of the good graphs to be counted.

For each test case, output one line: * One integer, the number of good graphs on $n$ vertices modulo $P$.

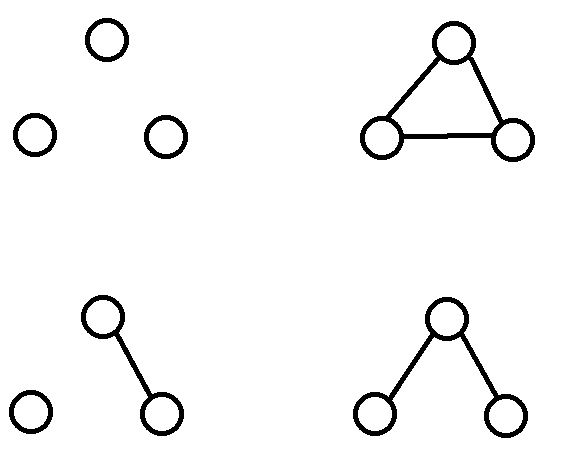
### Sample Explanation Below are all good graphs with $3$ vertices:  ### Constraints It is guaranteed that $T \leq 233$, $n \leq 23333$, $2^{29} < P < 2^{30}$, and $P$ is prime. ### Hint The time complexity of an algorithm that can pass this problem might be worse than you expect, or it might be better than you expect. ### Copyright Information From the 2018 Tsinghua University Programming Contest and Collegiate Invitational (THUPC2018). Thanks to [Pony.ai](http://pony.ai/) for supporting this contest. Resources such as editorials can be found at . Translated by ChatGPT 5