P5458 [BJOI2016] Crystal

Do not panic, none of today’s problems were made by Xiaoqiang. —A work poured with countless efforts, yet now he has to destroy it with his own hands. It is hard to understand how he feels. —There is no other choice. If the energy resonance is not removed... Looking at the crystals already planted with explosives, 02 put down the telescope and looked at the resonance analysis report in his hand. Some crystals will still survive... maybe.

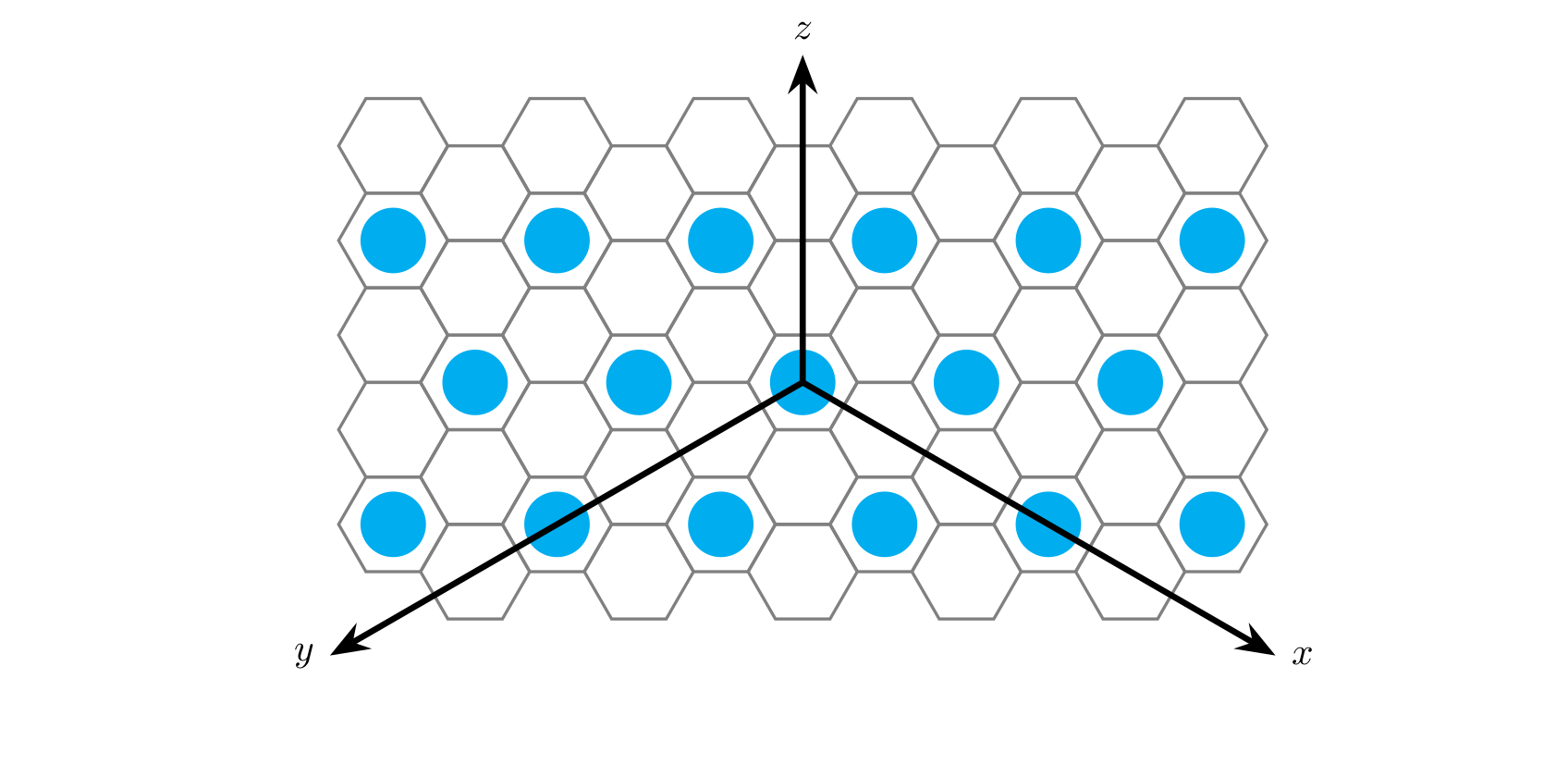
The map consists of densely tiled hexagonal cells, and each cell is adjacent to six other cells. For convenience, we use coordinates $(x,y,z)$ to describe the position of a cell: starting from the origin, walk several steps along the $x$, $y$, and $z$ directions as shown in the figure to reach that cell. It is possible that two coordinates describe the same cell. For example, $(1,1,1)$ and $(0,0,0)$ both describe the origin.  Clearly, cell $(x,y,z)$ is adjacent to $(x+1,y,z)$, $(x-1,y,z)$, $(x,y+1,z)$, $(x,y-1,z)$, $(x,y,z+1)$, and $(x,y,z-1)$. There are $N$ crystals located in the cells of the map. The $i$-th crystal is in the cell described by coordinates $(x_i, y_i, z_i)$ and has value $c_i$. A single cell may contain multiple crystals. On the map, some cells have energy sources installed. As shown below, any cell described by coordinates whose $x+y+z$ is a multiple of $3$ has an energy source installed.  The value of crystals in a cell with an energy source increases by an additional $10\%$. If the cells containing three crystals satisfy certain patterns, they will trigger resonance. There are two types of resonance: $a$ resonance and $b$ resonance. $a$ resonance: If the cells containing three crystals form a triangle such that every pair of cells is adjacent, then an $a$ resonance is triggered.  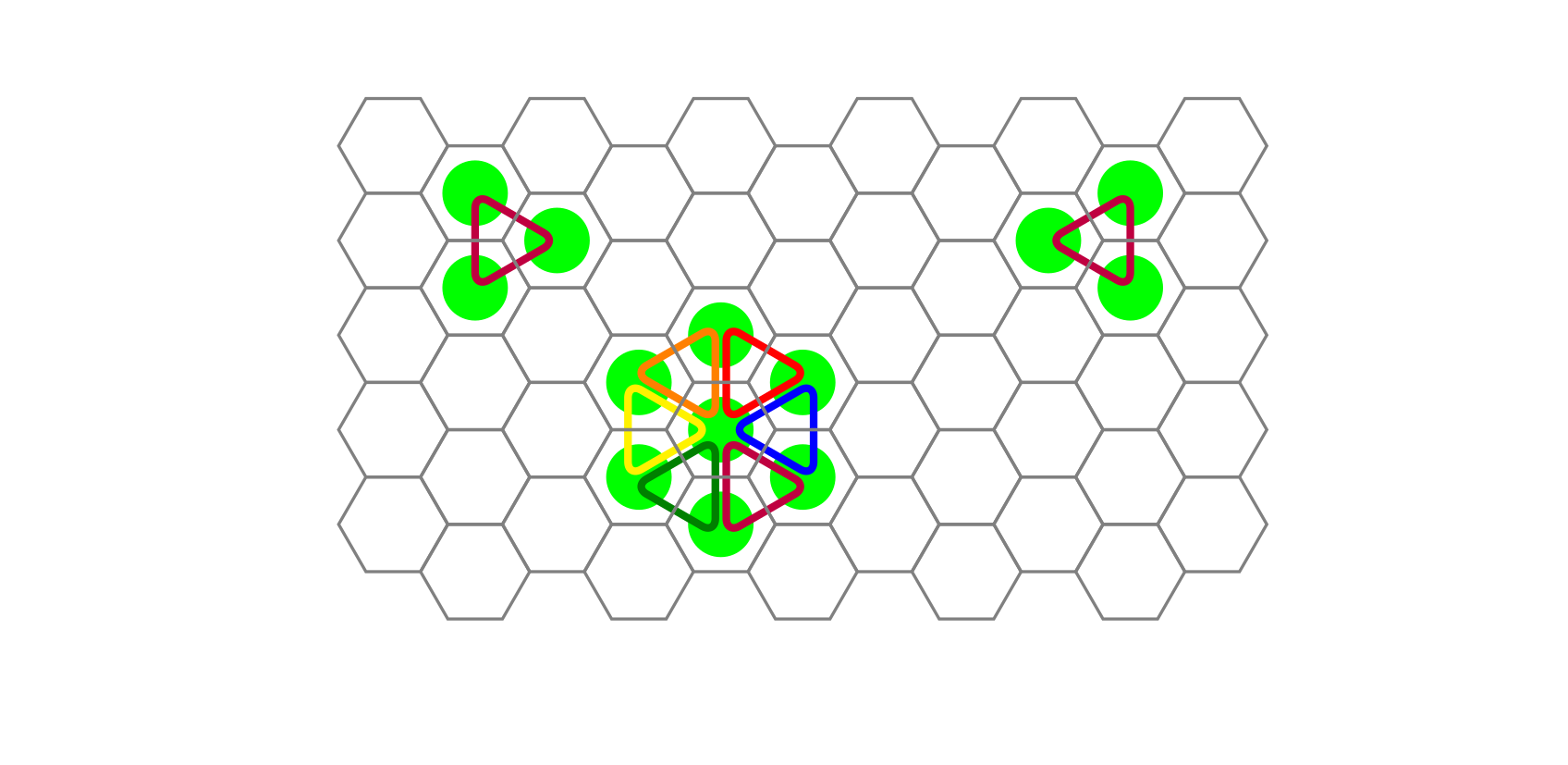In the figure, each triangle means that if each of the three cells contains one crystal, they will trigger one $a$ resonance. $b$ resonance: If the cells containing three crystals are arranged in a straight line segment of length $2$ such that consecutive cells are adjacent, and the middle cell has an energy source, then a $b$ resonance is triggered.  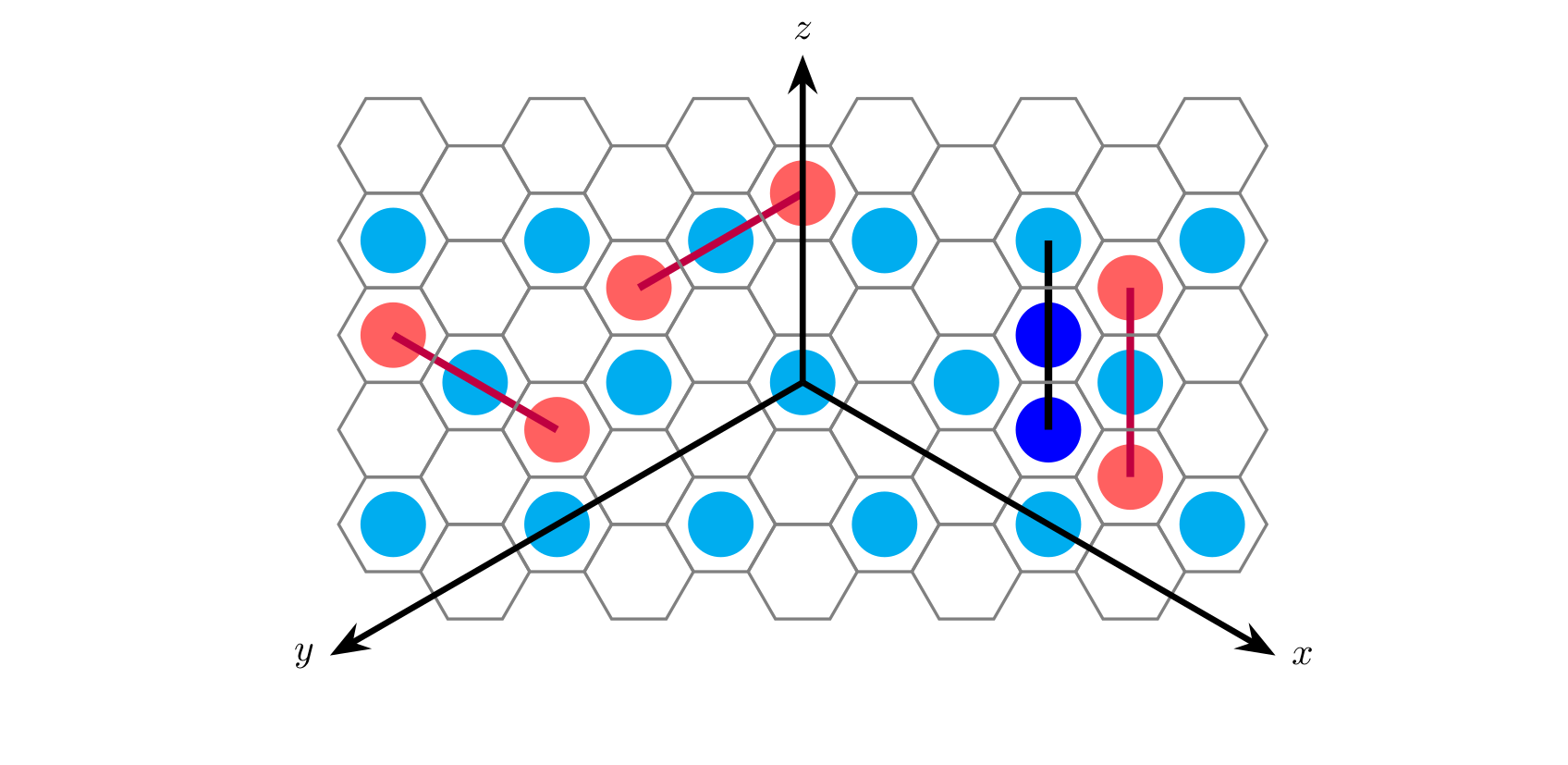In the figure, the pink segments indicate that if each of the three cells contains one crystal, they will trigger a $b$ resonance. The black segments indicate that even if these three cells contain crystals, they will not trigger a $b$ resonance. Now you need to blow up some crystals so that no resonance occurs, and under this condition, maximize the total value of the remaining crystals.

The first line contains a positive integer $N$, the number of crystals. The next $N$ lines each contain four integers separated by spaces: $x_i,y_i,z_i,c_i$, describing the position and value of a crystal. Different crystals may share the same position.

Output one real number in a single line: the total value of the remaining crystals, rounded to $1$ decimal place.

[Sample $1$ Explanation] Four crystals form a diamond shape. There is no $b$ resonance, and there are $2$ occurrences of $a$ resonance: the triangles formed by crystals $1,2,4$ and by crystals $1,3,4$. Therefore, to eliminate the two $a$ resonances, there are $3$ possible plans: 1. Blow up crystal $1$, keep crystals $2,3,4$, total remaining value $5+7+13=25$. 2. Blow up crystal $4$, keep crystals $1,2,3$, total remaining value $11 \times(1+10\%)+5+7=24.1$. 3. Blow up crystals $2,3$, keep crystals $1,4$, total remaining value $11 \times (1+10\%)+13=25.1$. So we choose the third plan, and the maximum total remaining value is $25.1$. [Constraints] $1\le N \le 50000$ $1\le c_i \le 1000$ $-1000 \le x_i,y_i,z_i \le 1000$ Translated by ChatGPT 5