P5465 [PKUSC2018] Interstellar Travel

There are $n$ planets, numbered from 1 to $n$. They are located in the same galaxy, which can be modeled as a number line. Each planet is a point on the number line. In particular, the coordinate of planet $i$ is $i$. At the beginning, due to technological limits, the residents of these $n$ planets could not communicate with each other, so they did not know each other existed. Now, these planets have independently developed tools for interstellar travel and interstellar communication. For planet $i$, by sending a powerful signal, it successfully made contact with all planets with indices in $[l_i,i-1]$ (planet 1 did not send any signal). Any two planets that make contact will build a **bidirectional** portal. For two planets $u,v$ that have a portal between them, residents on $u$ can spend 1 unit of time to teleport to $v$, and residents on $v$ can also spend 1 unit of time to teleport to $u$. Let $dist(x,y)$ denote the minimum time needed to travel from planet $x$ to planet $y$ through a sequence of portals between planets. Now there are $q$ interstellar merchants. The initial position of the $i$-th merchant is $x_i$, and his destination is one planet among $[l_i,r_i]$, where it is guaranteed that $l_i

The first line contains a positive integer $n$, representing the number of planets. The second line contains $n-1$ positive integers. The $i$-th positive integer is $l_{i+1}$, meaning that all planets with indices in the interval $[l_{i+1},i]$ have already made contact with planet $i+1$, and they can transmit to each other with cost 1. It is guaranteed that $l_{i+1}\leq i$. The third line contains a positive integer $q$, representing the number of queries. The next $q$ lines each contain three numbers $l_i,r_i,x_i$, meaning: choose a planet $y$ uniformly at random in $[l_i,r_i]$, and ask for the expected value of $dist(x_i,y)$. It is guaranteed that $l_i

For each query, note that the answer must be a rational number, so output it in the form $p/q$, requiring $\gcd(p,q)=1$. If the answer is an integer $m$, output $m/1$.

The undirected graph corresponding to the sample is as follows: 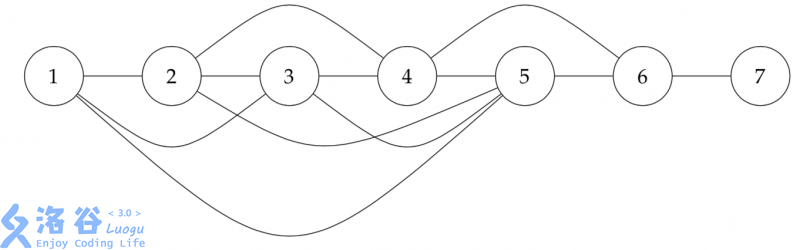 For $20\%$ of the testdata, $n \leq 100$. For another $25\%$ of the testdata, $n\leq 2000$. For another $25\%$ of the testdata, $n\leq 5000$. For $100\%$ of the testdata, $n,q\leq 3\times 10^5$. Translated by ChatGPT 5