P5472 [NOI2019] Douzhu Di

Time limit: 4 seconds. Memory limit: 512MB.

Xiao S is playing a game called “Dou Dizhu” with Xiao F. Poor Xiao S finds that he cannot beat Xiao F at playing cards, so he wants to do something during the shuffling stage. A deck has $n$ cards, numbered from top to bottom as $1 \sim n$. The **score** of the card numbered $i$ is $f(i)$. In this problem, $f(i)$ has exactly two possibilities: $f(i) = i$ or $f(i) = i^2$. The shuffling method is similar to what we do in daily life. We define it formally as follows: the shuffling stage consists of $m$ rounds, performed in order. In round $i$: 1. Xiao S takes the top $A_i$ cards from the deck. Then the deck is split into two piles: the first pile is the top $A_i$ cards, and the second pile is the remaining $n-A_i$ cards, and the relative order within each pile remains unchanged. In particular, when $A_i = n$ or $A_i = 0$, one pile is empty. 2. Next, merge the two piles to produce a new third pile. When the first pile has $X$ cards left and the second pile has $Y$ cards left, with probability $\dfrac{X}{X+Y}$ take the bottom card of the first pile and put it on the top of the new third pile; with probability $\dfrac{Y}{X+Y}$ take the bottom card of the second pile and put it on the top of the new third pile. 3. Repeat step $2$ until both piles are empty. This completes one round of shuffling. Because the shuffling process is random, Xiao S cannot know exactly which card is at a certain position. But after these $m$ rounds of shuffling, Xiao S wants to ask what the **expected score** of the card at a certain position is. Xiao S will ask you $Q$ such questions.

The first line contains three positive integers $n, m, type$, representing the number of cards, the number of shuffling rounds, and the type of $f(i)$. When $type = 1$, $f(i) = i$. When $type = 2$, $f(i) = i^2$. The next line contains $m$ integers, representing $A_1 \sim A_m$. The next line contains a positive integer $Q$, the number of queries from Xiao S. The next $Q$ lines each contain a positive integer $c_i$, meaning Xiao S wants to know the **expected score** of the card at the $c_i$-th position from top to bottom. It is guaranteed that $1 \leq c_i \leq n$.

Output $Q$ lines. Each line contains one integer, which is the answer modulo $998244353$. That is, suppose the answer in lowest terms is $\dfrac{a}{b}$, where $a$ and $b$ are coprime. Output an integer $x$ such that $bx \equiv a \pmod{998244353}$ and $0 \le x < 998244353$. It can be proven that such an integer $x$ is unique.

### More Samples You can obtain more samples through the additional files. #### Sample 2 See `landlords/landlords2.in` and `landlords/landlords2.ans` in the additional files. #### Sample 3 See `landlords/landlords3.in` and `landlords/landlords3.ans` in the additional files. ### Explanation for Sample Input/Output 1 - With probability $\dfrac{1}{4}$, the final result from top to bottom is $\{1, 2, 3, 4\}$. - With probability $\dfrac{1}{4}$, the final result from top to bottom is $\{1, 2, 4, 3\}$. - With probability $\dfrac{1}{4}$, the final result from top to bottom is $\{1, 4, 2, 3\}$. - With probability $\dfrac{1}{4}$, the final result from top to bottom is $\{4, 1, 2, 3\}$. So in the end, with probability $\dfrac{1}{4}$ the first position is $4$, and with probability $\dfrac{3}{4}$ the first position is $1$. Therefore, the expected score of the first position is $\dfrac{7}{4}$. 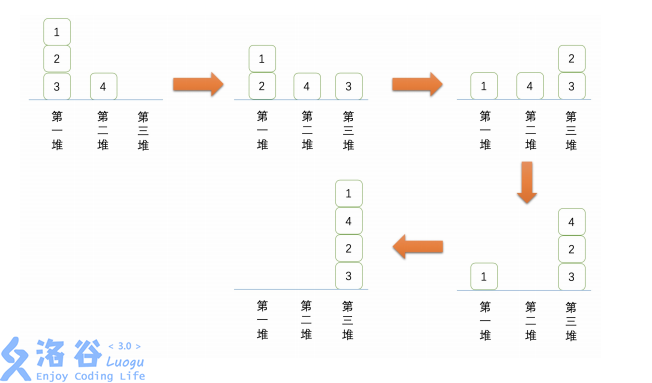To help you understand the shuffling process more intuitively, we draw below the process where the result is $\{1, 4, 2, 3\}$.  ### Constraints and Notes For all test points, it is guaranteed that $3\le n \le 10^7$, $1\le m,Q\le5\times 10^5$, $0\le A_i\le n$, $type\in \{1,2\}$. The specific limits for each test point are shown in the table below: | Test Point | $n$ | $m$ | $type=$ | Other Properties | | :----------: | :----------: | :----------: | :----------: | :----------: | | $1$ | $\le 10$ | $\le 1$ | $1$ | None | | $2$ | $\le 80$ | $\le 80$ | $1$ | None | | $3$ | $\le 80$ | $\le 80$ | $2$ | None | | $4$ | $\le 100$ | $\le 5\times 10^5$ | $2$ | All $A_i$ are the same | | $5$ | $\le 10^7$ | $\le 5\times 10^5$ | $1$ | None | | $6$ | $\le 10^7$ | $\le 5\times 10^5$ | $1$ | None | | $7$ | $\le 10^7$ | $\le 5\times 10^5$ | $1$ | None | | $8$ | $\le 10^7$ | $\le 5\times 10^5$ | $2$ | None | | $9$ | $\le 10^7$ | $\le 5\times 10^5$ | $2$ | None | | $10$ | $\le 10^7$ | $\le 5\times 10^5$ | $2$ | None | Please note that we do not guarantee $Q\le n$. ### Hint Here we give the definition of the expectation $\mathbb{E}[x]$ of a discrete random variable $X$: Suppose the possible values of $X$ are $X_1,X_2,\ldots X_k$, and $Pr[X_1],Pr[X_2],\ldots,Pr[X_k]$ are the probabilities that $X$ takes the corresponding values. Then the expectation of $X$ is: $$\mathbb{E}[x]=\sum^k_{i=1}X_i\times Pr[X_i]$$ Translated by ChatGPT 5