P5517 [MtOI2019] Gensokyo Mathematics Contest

The annual Gensokyo Mathematics Contest (thMO) is about to begin again. The young (actually old) girls (actually housewives) who study math in Gensokyo, together with the ice fairy baka, are preparing for thMO. But at that moment, the day-by-day peace of Gensokyo was broken. On the radio, a song of death started playing! At that moment, people recalled the fear of being ruled by arithmetic again. Only the voice of baka, baka, baka, baka echoed throughout Gensokyo. --- Kawashiro Nitori is sitting in the thMO2019 exam room! Because Nitori has her [supercomputer](https://www.luogu.org/problemnew/show/P4911), after successfully covering it with optical camouflage, she became unstoppable in the thMO2019 exam. * Nitori used her supercomputer to solve this problem in $0 \,\mathrm{ms}$: * $\exists \{ a_n\} (n=0,1,\cdots ,10^{18})$，given $a_0=2,a_1=5,a_{n+2}=3a_{n+1}-2a_n$, find $a_n\bmod 10^{9}+7$ * Nitori: Obviously, this can be done with matrix multiplication + fast exponentiation, and you can pass it in $O(\log n)$, roughly like this: $$ \begin{bmatrix} a_n & a_{n+1} \end{bmatrix}=\begin{bmatrix} a_0 & a_1 \end{bmatrix} \times \begin{bmatrix} 3 & 1 \\ -2 & 0 \end{bmatrix}^n $$ But Nitori encountered a problem she cannot solve, and she is asking for your help!

There exists a sequence $\{ a_n\} (n\in \{ 0,1,2,\cdots ,2^{64}-1\} )$. Given $a_0=-3,a_1=-6,a_2=-12,a_n=3a_{n-1}+a_{n-2}-3a_{n-3}+3^n$. * Now you are given a non-negative integer $n$. Let $p=10^{9}+7$. Please compute $a_n \bmod p$. * **Note: if $a_n 29; sd ^= sd

The first line contains three integers: $T$, $seed$, and $op$.

Output one integer: the **xor sum** of the answers to the $T$ queries.

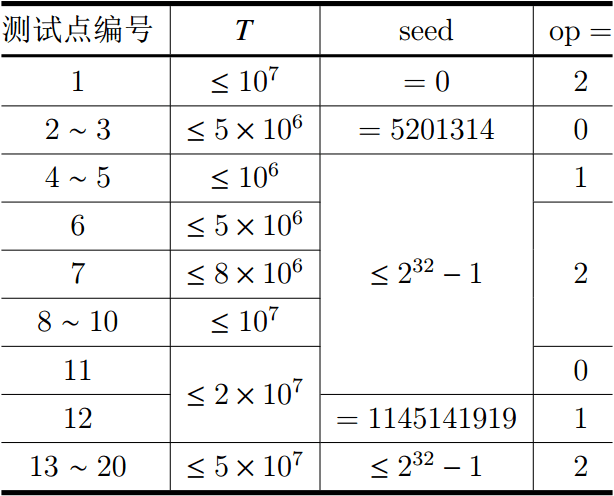
### Subtasks  ### Source [Lost Home 2019 League](https://www.luogu.org/contest/20135) (MtOI2019) T4 Problem setter: disangan233 Problem tester: suwakow Translated by ChatGPT 5