P5517 [MtOI2019] 幻想乡数学竞赛

一年一度的幻想乡数学竞赛 (thMO) 又要开始了。 幻想乡中学习数学的少 (lao) 女 (tai) 们 (po) 和冰之妖精 baka 一起准备着 thMO。 但是在那一刻，幻想乡日复一日的宁静被打破了。 广播里，播放起了死亡的歌曲！ 在那一刻，人们又回想起了被算数支配的恐惧。 就剩下 baka，baka，baka，baka 的声音在幻想乡里回荡。 --- 河城 荷取 (Kawashiro Nitori) 正坐在 thMO2019 的考场上！ 因为荷取有着她的[超级计算机](https://www.luogu.org/problemnew/show/P4911)，在成功地用光学迷彩覆盖了计算机之后，荷取在 thMO2019 的考场上所向披靡。 * 荷取用她的超级计算机 $0 \,\mathrm{ms}$ 跑出了这么一道题： * $\exists \{ a_n\} (n=0,1,\cdots ,10^{18})$，已知 $a_0=2,a_1=5,a_{n+2}=3a_{n+1}-2a_n$，求 $a_n\bmod 10^{9}+7$ * 荷取：显然，这个题可以用矩阵乘法 + 快速幂，可以 $O(\log n)$ 水过去，差不多就这样： $$ \begin{bmatrix} a_n & a_{n+1} \end{bmatrix}=\begin{bmatrix} a_0 & a_1 \end{bmatrix} \times \begin{bmatrix} 3 & 1 \\ -2 & 0 \end{bmatrix}^n $$ 但是荷取遇到了一道她不会的题，她正在寻求你的帮助呢！

存在一个数列 $\{ a_n\} (n\in \{ 0,1,2,\cdots ,2^{64}-1\} )$。 已知 $a_0=-3,a_1=-6,a_2=-12,a_n=3a_{n-1}+a_{n-2}-3a_{n-3}+3^n$。 * 现在给你一个非负整数 $n$ ，令 $p=10^{9}+7$，请你求出 $a_n \bmod p$。 * **注：若 $a_n 29; sd ^= sd

第一行三个整数，输入 $T$ ， $seed$ 和 $op$。

第一行一个整数，输出 $T$ 组询问的答案的**异或和**。

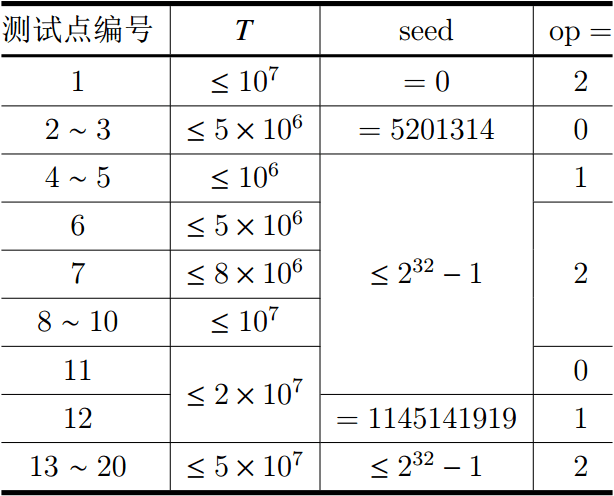
### 子任务  ### 题目来源 [迷途之家 2019 联赛](https://www.luogu.org/contest/20135)(MtOI2019) T4 出题人：disangan233 验题人：suwakow