P5521 [yLOI2019] Deep in the Plum Forest, Winter Is Nowhere to Be Seen

> The wind blows up the deep winter of Meiling; the frost surges like raging waves; > The snow falls and burns everything into emptiness, like this dream that cannot be caught. > When I wake up, many years have passed; the bronze rings on the palace gates have grown rusty, and sorrow begins to grow as well. — Yin Lin, *Deep in the Plum Forest, Winter Is Nowhere to Be Seen*.

Fu Su walks out of the deep winter Meiling and arrives at a rooted tree with $n$ nodes. If you do not know what a tree is, you may think of it as a simple undirected connected graph whose number of edges is exactly one less than the number of nodes. If we specify that $x$ is the root of a tree $T$, then for any node $y$, the path from $y$ to the root is defined as the set of nodes passed through when starting from $y$ and reaching $x$ without visiting any node twice. It can be proven that such a set is unique. A node $u$ is a child of node $v$ if and only if $u$ is connected to $v$ and $u$ is not on the path from $v$ to the root. If $u$ is a child of $v$, then $v$ is the parent node of $u$. If I were a ~~toxic~~ genius like @[\_rqy](https://www.luogu.org/space/show?uid=7868), I might ask you how many labeled unrooted trees with $n$ nodes exist such that every node has at most $k$ children. Unfortunately I cannot solve that either, so I will not ask such a painful question. Fu Su starts from node $1$ of this $n$-node tree and walks along the edges. We define node $1$ as the root of the tree. His movement rule is: when Fu Su is at node $u$, he either chooses a node $v$ among the children of $u$ that he has **not visited** and moves to $v$, or he chooses to return to the parent node of $u$. Now each node has a weight $w$, where the weight of node $i$ is $w_i$. He wants to place plum blossoms brought from Meiling onto some node of the tree. We say Fu Su can place plum blossoms on node $u$ if and only if the following conditions are satisfied: > Fu Su is currently at node $u$. > > For every child $v$ of $u$, node $v$ has been placed with $w_v$ plum blossoms. Meanwhile, Fu Su can take back the plum blossoms on **any node** at **any time**, and he does not need to walk to that node when taking them back. Now Fu Su asks you: for each node, if he wants to place $w_i$ plum blossoms on node $i$, what is the minimum number of plum blossoms he needs to bring out from Meiling?

Each input file contains one and only one set of testdata. The first line contains an integer $n$, the number of nodes in the tree. The second line contains $n - 1$ integers separated by spaces. The $i$-th integer $p_i$ denotes the index of the parent of node $i + 1$. The third line contains $n$ integers separated by spaces. The $i$-th integer denotes $w_i$.

Output one line with $n$ integers separated by spaces. The $i$-th integer denotes the number of plum blossoms that need to be prepared to place $w_i$ plum blossoms on node $i$.

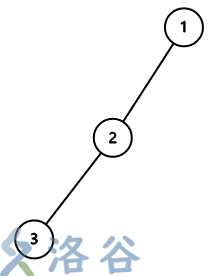
#### Explanation for Sample Input/Output 1  The input of Sample 1 is shown in the figure above. Every node needs to be placed with one plum blossom. If we place plum blossoms on node $1$, we move from node $1$ to node $2$, then to node $3$, place one plum blossom on node $3$, return to node $2$, place one plum blossom on node $2$, and at the same time take back the plum blossom on node $3$. Then return to node $1$, and place the plum blossom taken back from node $3$ onto node $1$. In total, we need two plum blossoms. The plans for placing plum blossoms on nodes $2$ and $3$ are similar. 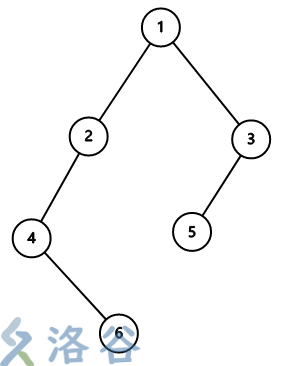#### Explanation for Sample Input/Output 3  The input of Sample 3 is shown in the left figure. First move from node $1$ to node $3$, then to node $5$, place $12$ plum blossoms on node $5$, then return to node $3$, place $1$ plum blossom on node $3$, take back the $12$ plum blossoms on node $5$, and return to node $1$. Then move to node $2$, and move through node $4$ to node $6$, place $15$ plum blossoms, return to node $4$ and place $5$ plum blossoms. At this moment, the number of plum blossoms on the tree is $5 + 15 + 1 = 21$, located at nodes $4$, $6$, and $3$. Then take back the plum blossoms on node $6$, return to node $2$, place $14$ plum blossoms, take back the blossoms on node $4$, return to node $1$, and place $3$ plum blossoms on node $1$, thus achieving the goal of placing plum blossoms on node $1$. It can be verified that the minimum cost is $21$. The answers for other nodes are similar. Please note that the answers for other nodes are not necessarily obtained by walking along the movement path of that node. --- #### Constraints and Agreements | Test Point ID | $n = $ | Test Point ID | $n = $ | | :----------: | :------: | :----------: | :------: | | 1 | $1$ | 11 | $100003$ | | 2 | $8$ | 12 | $100003$ | | 3 | $8$ | 13 | $100003$ | | 4 | $8$ | 14 | $100003$ | | 5 | $8$ | 15 | $100004$ | | 6 | $100000$ | 16 | $100004$ | | 7 | $100000$ | 17 | $100004$ | | 8 | $100002$ | 18 | $100004$ | | 9 | $100002$ | 19 | $100004$ | | 10 | $100002$ | 20 | $100004$ | - For test points 5 and 6, a special property holds: each node has at most $2$ child nodes. - For test points 8 to 10, a special property holds: each node has at most $5$ child nodes. - For test points 11 to 14, a special property holds: the number of nodes on the path from any node to the root is at most $3$, i.e. the height of the tree is at most $3$. - For $100\%$ of the data, it is guaranteed that $1 \leq n \leq 10^5 + 4,~1 \leq p_i \leq i,~1 \leq w_i \leq 1000$. --- #### Hint - The last digit of $n$ can help you quickly determine the special property of the test point. Translated by ChatGPT 5