P5525 [Ynoi2012] WC2016 Full of Disappointment

In the 2D Cartesian coordinate system, You are given $n$ points. These $n$ points are reachable. If points $A, B$ are reachable, then all points on the segment $AB$ are also reachable. You are given $m$ circles. Determine which circles satisfy that every point inside the circle is reachable.

The first line contains an integer $T$, which indicates the number of test cases. Then there are $T$ test cases. For each test case: The first line contains an integer $n$. The next $n$ lines each contain two integers $x_i, y_i$, representing a point. The next line contains an integer $m$. The next $m$ lines each contain three integers $X_i, Y_i, R_i$, representing a circle.

For each test case, output one line: a `01` string of length $m$, representing the answers (`0` means there exists an unreachable point inside the circle, `1` means all points inside the circle are reachable).

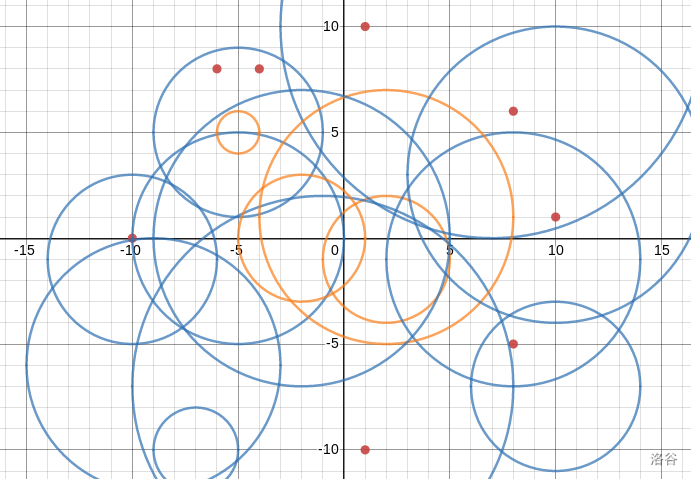
Idea: ccz181078, Solution: ccz181078, Code: ccz181078, Data: ccz181078. Sample explanation: The red points are the points given in the sample. The orange circles indicate queries with answer `1`, and the blue circles indicate queries with answer `0`.  Constraints: $1\leq n,m\leq 5\times 10^5$, $1\leq R_i\leq 10^6$, $-10^6\leq x_i,y_i,X_i,Y_i\leq 10^6$, $\sum n\leq 5\times 10^5$, $\sum m\leq 5\times 10^5$. It is guaranteed that when $R_i$ changes by no more than $1$, the answer does not change. Translated by ChatGPT 5