P5530 [BalticOI 2002] Bitonic Paths.

Nowadays, road toll systems are developing fast. The density of roads is getting higher and higher, so choosing the best route is a very practical problem. The roads in a city are bidirectional. Each road has a fixed travel time and a fee that must be paid. A path is made up of consecutive roads. The total time is the sum of travel times of all roads on the path, and the total fee is the sum of fees paid on all roads on the path. A path is better if it is faster, or if it costs less. More strictly, if one path is faster than another path and does not require paying more, then it is better. The reverse can be understood in the same way. If no path is better than a given path, then this path is called a minimal path. Such minimal paths may be more than one, or there may be no path at all. Task: given the network, compute the total number of minimal paths. Two minimal paths with the same fee and time are counted as one. You only need to output the number of different types of minimal paths.

The first line contains four integers: the number of cities $n$, the number of roads $m$, and the start and end cities $s, e$. $\newline$ The next $m$ lines each describe one road: its two endpoints $p, r$, the fee $c$, and the time $t$. $\newline$ There may be multiple roads connecting the same pair of cities.

Output one line with one integer, representing the total number of minimal paths.

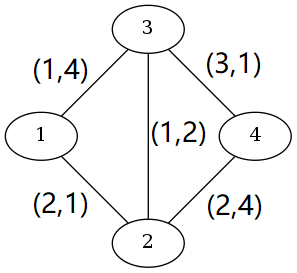
**Constraints:** - $1\leq{n}\leq100$, $0\leq{m}\leq300$. - $1\leq{s,e,p,r}\leq{n}$, $0\leq{c,t}\leq100$. - $s\neq{e}$, $p\neq{r}$. **Sample Explanation:**  There are $4$ paths from $1$ to $4$: $1\rightarrow 2\rightarrow 4$ (fee $4$, time $5$), $1\rightarrow 3\rightarrow 4$ (fee $4$, time $5$), $1\rightarrow 2\rightarrow 3\rightarrow 4$ (fee $6$, time $4$), and $1\rightarrow 3\rightarrow 2\rightarrow 4$ (fee $4$, time $10$). $1\rightarrow 3\rightarrow 4$ and $1\rightarrow 2\rightarrow 4$ are better than $1\rightarrow 3\rightarrow 2\rightarrow 4$. There are two types of best paths: fee $4$, time $5$ ($1\rightarrow 2\rightarrow 4$ and $1\rightarrow 3\rightarrow 4$), and fee $6$, time $4$ ($1\rightarrow 2\rightarrow 3\rightarrow 4$). Translated by ChatGPT 5