P5560 [Celeste-B] Golden Feather

> That is it, Madeline. > Keep breathing. You can do it.

"Your breathing keeps that feather floating." "Breathe steadily and slowly. Inhale, exhale." "See, it is this easy every time." As Madeline breathes, the feather moves up and down. From her observation, Madeline also found that the feather seems to follow a strange trajectory. In each round of breathing, the feather stops at certain places. These places are magical. Specifically, the magic value of the $i$-th stop is $(i+1)^2-1$. Also, when a round of breathing ends, the feather seeps out some energy. As long as she can use this energy to connect these stopping places, Madeline can use the feather's power to fly. More specifically, due to "like repels like", the more similar the magic values of two places are, the harder it is to connect them. The energy required to connect two places is the $gcd$ of their magic values. With one breath after another, Madeline has no time to compute the minimum energy needed. Since the energy seeping out of the feather is limited, can you help her compute the minimum energy needed to connect these places where the feather stops?

The first line contains a positive integer $T$, indicating the number of breathing rounds. The next $T$ lines each contain a positive integer $n$, indicating the number of stopping places of the feather in that round.

Output $T$ lines, one integer per line, representing the minimum energy required.

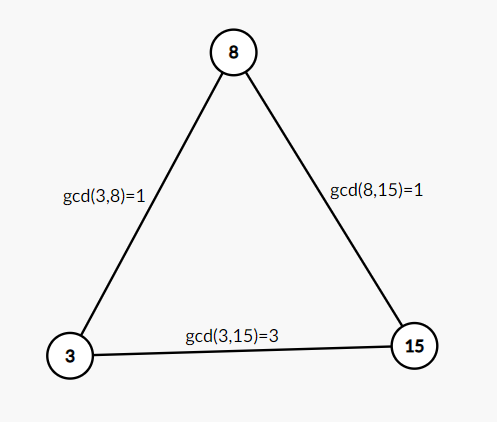
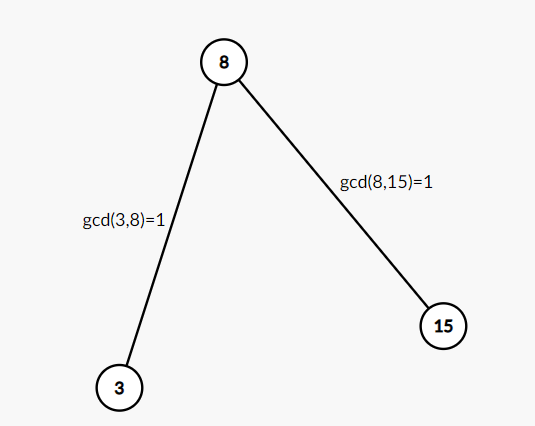
The sample explanation for $n=3$ is shown in the figures below.   Constraints: For $5\%$ of the testdata, $n \leq 3$. For $10\%$ of the testdata, $n \leq 1000$. For $50\%$ of the testdata, $n \leq 10^6$, $T \leq 10$. For $100\%$ of the testdata, $n \leq 10^{18}$, $T \leq 100$. Translated by ChatGPT 5