P5564 [Celeste-B] Say Goodbye

> You actually made it through. It is hard to believe, is it not? > The process of working hard was pretty interesting. > Well then, > What are you waiting for?

Madeline shared the strawberries she collected with her friends. The bright red strawberries and the golden yellow strawberries were mixed together, and her friends liked them very much. To thank Madeline, her friends collected many colorful beads and planned to string them into a colorful necklace as a gift for Madeline. After careful preparation, there are now $n$ beads on the table. These beads have $k$ colors in total. Specifically, there are $a_i$ beads of the $i$-th color. Looking at the crystal-clear beads on the table, the friends are now troubled, because they do not know how to string them together to make it the most beautiful. They ask you for help: compute the total number of essentially different plans. They cannot tell the order of beads apart, so **two beads are different only if their colors are different**. This necklace must be complete, so **all beads form one connected component**. The necklace also cannot be too messy, so all beads must form a **unicyclic graph (基环树)**. After asking Madeline’s friends many times, you find that two subtrees of this unicyclic graph are different if and only if **the colors of their corresponding nodes are different, or the two subtrees have different structures**. Different subtrees are considered ordered. For example, the following **partial** stringing methods are all different from each other.  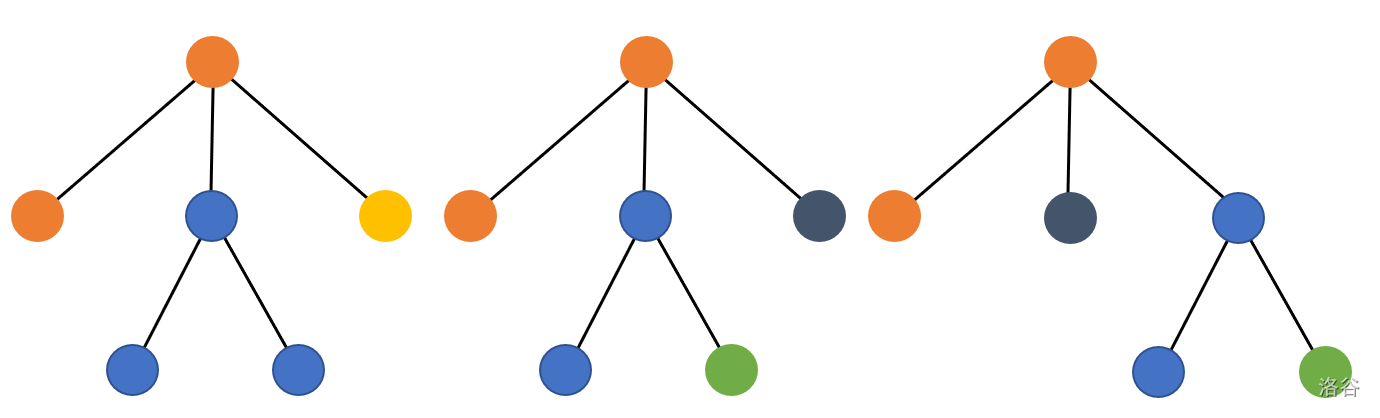The friends are in a hurry, so if two necklaces can become the same by **rotating the cycle (基环)**, then these two necklaces are essentially the same.

The first line contains two integers $n, k$, representing the total number of beads and the number of colors. The next line contains $k$ integers $a_i$, representing the number of beads of each color.

Output one integer, the number of plans modulo $998244353$.

Unicyclic graph (基环树): a connected graph with $n$ vertices and $n$ edges, **with no self-loops**. It is easy to see that such a graph consists of a cycle with some trees attached to it. Cycle (基环): the cycle in a unicyclic graph. For $5\%$ of the testdata, $n \leq 8$. For another $10\%$ of the testdata, $k = 1$ and $n \leq 10^3$. For the first $30\%$ of the testdata, $n \leq 10^3$. For another $20\%$ of the testdata, $k = 1$ and $n \leq 5 \times 10^4$. For the first $80\%$ of the testdata, $n \leq 5 \times 10^4$. For $100\%$ of the testdata, $a_i > 0$, $\sum a_i = n$, $n \leq 2 \times 10^5$, and $k \leq n$. 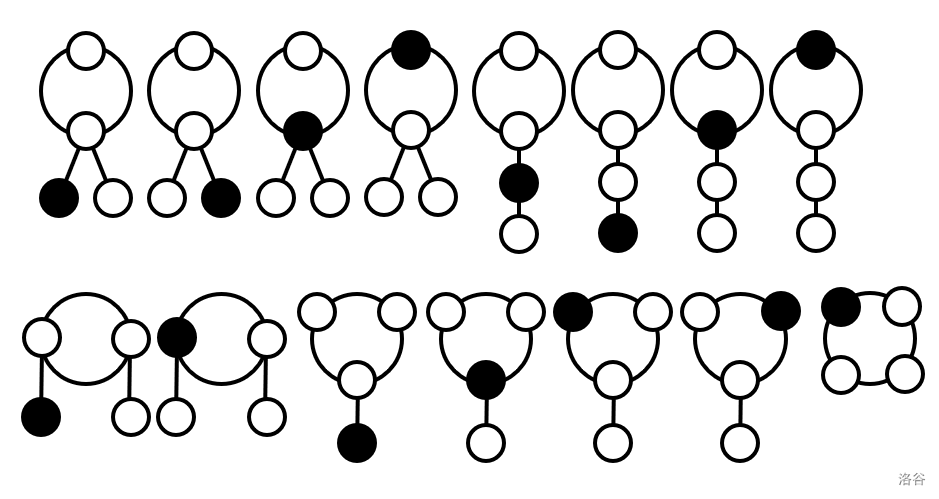Explanation for the second sample: There are $15$ cases as follows:  Translated by ChatGPT 5