P5573 [CmdOI2019] Interstellar KFC 3-on-3 Basketball Tournament

In the year $3100$, the Earth Federation’s galaxy contains $N$ planets that have completed a massive road construction project, upgrading from the original $N-1$ bidirectional spacetime tunnels to an **undirected complete graph**. Louis Paosen is an interstellar traveler. Last time you helped him solve a difficult problem (when you ~~were crushing teams~~), so he has come to ask for your help again.

Still due to funding concerns, the Earth Federation could not build every road perfectly. Traveling through a road **requires certain ship performance**. Louis Paosen is hosting a grand KFC 3-on-3 basketball tournament within the federation. For a time, many players from different planets rushed to participate. Three kinds of ships (types A/B/C) are being heavily promoted inside the Earth Federation. Because they took advertising money, team formation requires that among the $3$ people: the first uses type A, the second uses type B, and the third uses type C (so they can get bonus points). Now there are many 3-person teams preparing to join. They have their ships ready (meeting the bonus condition), but they may come from different planets. Due to ship performance limits, they may not be able to gather together on some planet. Because the manufacturing processes of these three companies are very different, ships have very different tolerance to the environment of the same road, following a strange rule. Node $u$ has three sets of coefficients $P_A[u],P_B[u],P_C[u]$. The passing difficulty of edge $u\leftrightarrow v$ is: $$\begin{cases}\text{Type A ship passing difficulty}=P_A[u]\ {\rm xor}\ P_A[v]\\\text{Type B ship passing difficulty}=P_B[u]\ {\rm xor}\ P_B[v]\\\text{Type C ship passing difficulty}=P_C[u]\ {\rm xor}\ P_C[v]\end{cases}$$ A ship can pass an edge only when its performance index is not less than the passing difficulty of that edge for the corresponding type (see the sample explanation for details). Louis Paosen has prepared a match venue on every planet, so for each 3-person team, you only need to output the number of feasible gathering planets.

The first line: $n,q$. Lines 2 to 4: $P_A[1\sim n],P_B[1\sim n],P_C[1\sim n]$. The next $q$ lines: each line contains six numbers $h_A,u_A,h_B,u_B,h_C,u_C$, representing the ship performance and the starting planet index for each of the three members of a team.

For each 3-person team, output one line with one number: the number of feasible gathering planets.

| ID | $n$ | $q$ | ① | ② | ③ | | :--: | :--: | :--: | :--: | :--: | :--: | | #1-3 | $100$ | $100$ | - | - | - | | #4 | $4\times 10^4$ | $4\times 10^4$ | * | * | * | | #5 | $4\times 10^4$ | $4\times 10^4$ | * | * | - | | #6 | $4\times 10^4$ | $4\times 10^4$ | * | - | * | | #7 | $4\times 10^4$ | $4\times 10^4$ | * | - | - | | #8 | $4\times 10^4$ | $4\times 10^4$ | - | - | - | | #9 | $4\times 10^4$ | $8\times 10^4$ | - | - | * | | #10~13 | $4\times 10^4$ | $8\times 10^4$ | - | - | - | - Property ①: $P_C[1\sim n]$ are all equal. - Property ②: $P_B[1\sim n]$ are all equal. - Property ③: $P_A[1\sim n], P_B[1\sim n], P_C[1\sim n]\in \{0,1\}$. (#1~#9 are $6$ points each, #10~#13 are $46$ points total; #1~#7 have a memory limit of 500MB, and the remaining test points have a memory limit of 125MB). All numbers in the input are integers within $[0,10^8]$. 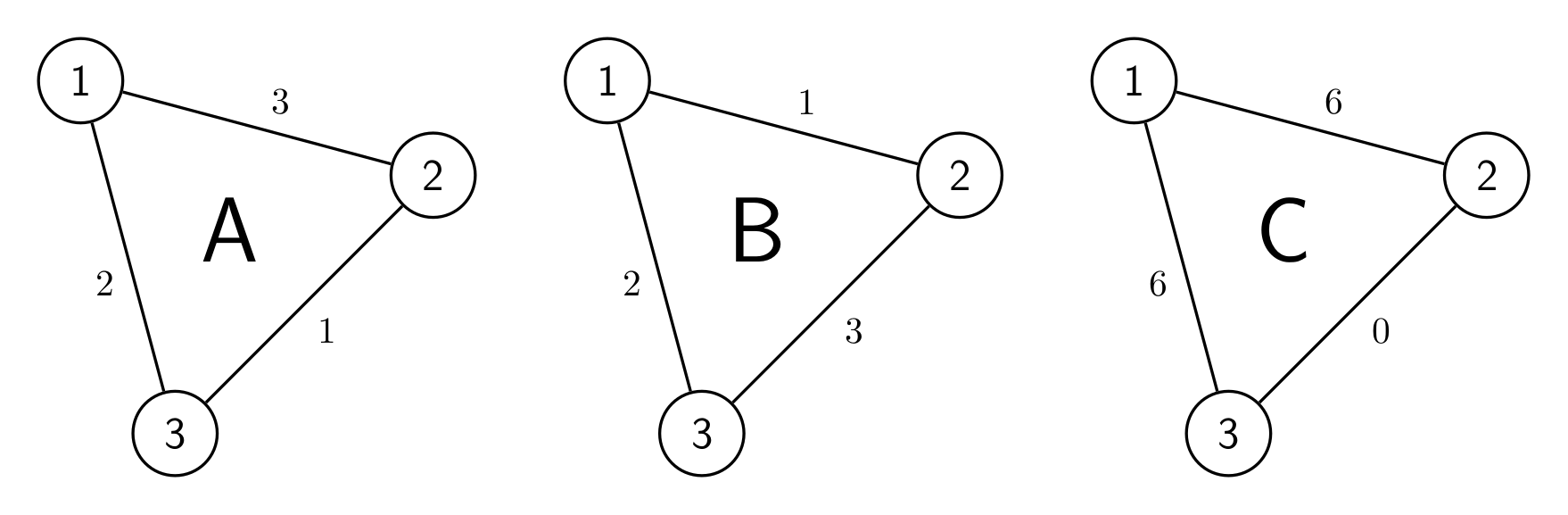### Sample 1 Explanation  The three performance graphs are shown above. For the A graph, $\begin{cases}(1,2)=P_A[1]\ {\rm xor}\ P_A[2]=3;\\(1,3)=P_A[1]\ {\rm xor}\ P_A[3]=2;\\(2,3)=P_A[1]\ {\rm xor}\ P_A[2]=1;\end{cases}$ (The edges are generated by XOR-ing the three arrays.) The first team: - The type A ship starting from $1$ has performance as high as $5$, and can reach all planets. - The type B ship starting from $2$ has performance only $2$, cannot pass $(3,2)=3$, but can still reach all planets. - The type B ship starting from $3$ has performance only $3$, can only pass $(2,3)=0$, and can reach planets $2,3$. - Therefore, the number of planets that all members of the first team can reach is $2$. Translated by ChatGPT 5