P5588 小猪佩奇爬树

佩奇和乔治在爬♂树。 给定 $n$ 个节点的树 $T(V,E)$，第 $i$ 个节点的颜色为 $w_i$，保证有 $1 \leq w_i \leq n$。 对于 $1 \leq i \leq n$，分别输出有多少对点对 $(u,v)$，满足 $u

第一行 $1$ 个正整数，表示 $n$ 。 第二行 $n$ 个正整数，第 $i$ 个正整数表示 $w_i$。 之后 $n-1$ 行，每行 $2$ 个正整数 $u,v$，表示 $T$ 中存在边 $(u,v)$。

共 $n$ 行，每行 $1$ 个正整数，第 $i$ 行输出包含所有颜色为 $i$ 的节点的路径个数。

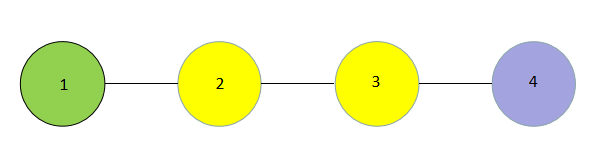
 对于第一组样例而言。 对于颜色 $1$，点对 $(1,2),(1,3),(1,4)$ 满足条件。 对于颜色 $2$，点对 $(1,3),(1,4),(2,3),(2,4)$ 满足条件。 对于颜色 $3$，点对 $(1,4),(2,4),(3,4)$ 满足条件。 对于颜色 $4$，由于图中没有颜色为 $4$ 的节点，所以所有点对均满足条件。 ### 数据范围 对于 $40\%$ 的数据，$n \leq 10^2$。 对于 $60\%$ 的数据，$n \leq 10^3$。 对于 $100\%$ 的数据，$n \leq 10^6$。