P5628 [AFOI-19] Meetup

After lunch, a group of people planned to go check the exam venue. IY, SY, QM, MY, and UU had already agreed to meet up that afternoon. Then everyone unanimously decided to dump the responsibility of planning the trip onto IY. (IY: ???? Why me?) (QM: I’ll give you candy.) (IY: Okay, no problem. Leave it to me.)

The city where IY lives has $n$ intersections, and $n - 1$ roads connect these intersections. The roads are bidirectional. In other words, the city forms a tree. The distance between two different intersections is defined as the number of roads on the simple path between them, and the distance from an intersection to itself is $0$. We also define the importance of a road. If a road becomes unusable and this causes $t$ pairs of intersections to be unable to reach each other, then $t$ is the importance of that road. 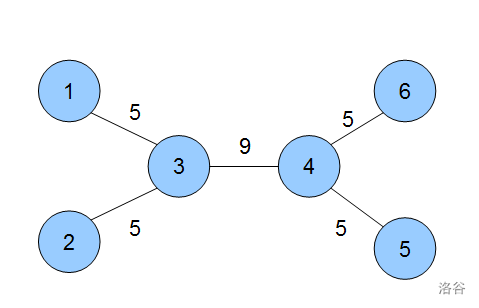As shown in the figure below:  The importance of the road between $(3,4)$ is $9$. This is because for $(1,4)$, $(2,4)$, $(3,4)$, $(1,5)$, $(2,5)$, $(3,5)$, $(1,6)$, $(2,6)$, $(3,6)$ to reach each other, they all must pass through this edge. IY received some very bad news: one intersection is under construction (but IY does not know where). The construction affects the area within distance $k$ from the construction point, and all intersections whose distance to the construction point is less than or equal to $k$ have been completely closed. This means the group cannot pass through the affected intersections or the roads directly connected to these intersections. IY has to consider the worst case. Since he does not know the construction location, he wants to know what the maximum possible total importance of the affected roads is.

The first line contains two integers $n, k$. The next $n - 1$ lines each contain two integers $u, v$, describing a road, meaning that intersection $u$ is directly connected to intersection $v$.

Output one integer, representing the maximum value of the total importance of the affected roads.

- **Sample Explanation** Sample $1$: This is the example shown in the statement. If the construction location is at intersection $3$ or $4$, then the total importance of the affected roads is $19$. No value larger than $19$ can be found. Sample $2$: It satisfies the special property of being a chain. - **Constraints** For the first $20\%$ testdata, $n \le 100, 0 \le k \le 7$. For the first $40\%$ of the data: the data is guaranteed to be random. Specially, the third test point has only $k == 0$. For $100\%$ of the data: $n \le 30000, 0 \le k \le 200$. Specially, the tenth test point degenerates from a tree into a chain. Translated by ChatGPT 5