P5629 [AFOI-19] Intervals and Division

SY finally managed to solve the math problem QM gave her. Right at lunchtime, QM stuffed an imaginary bubble into her mind… SY popped it and saw yet another long string of numbers! SY really does not want to think anymore, so she decides to use elementary-school division to wipe out the numbers in her head.

Define the operation $op$ as: divide the current number by $d$ and take the floor. SY now has $m$ “original numbers”. If a number can become an “original number” after performing the $op$ operation some number of times (including $0$ times), then this number can be wiped out by that “original number”. Note that “original numbers” will not be consumed. Now SY asks you: for an interval $[l,r]$, under the condition that you wipe out as many numbers as possible, what is the minimum number of “original numbers” needed?

The first line contains $4$ numbers $n,m,d,q$, representing the number of elements in the sequence $\{a\}$, the number of “original numbers” SY has, the parameter of the $op$ operation, and the number of queries. The second line contains the sequence $\{a\}$, i.e., the numbers that need to be wiped out. The third line contains $m$ “original numbers”. The next $q$ lines each contain two numbers $l$ and $r$, indicating the query interval $[l,r]$.

In the order of the queries, output one integer per line as the answer.

#### Sample Explanation: **Sample 1**: $20$ can become $6$ after one $op$ operation (divide by $3$ and take the floor), but $0$ cannot become $6$ after any number of $op$ operations. So for interval $[1,1]$, at most $0$ numbers can be wiped out; under the condition of wiping out the maximum number of numbers, the minimum number of “original numbers” needed is $0$. For intervals $[1,2]$ and $[2,2]$, at most $1$ number can be wiped out; under that condition, the minimum number of “original numbers” needed is $1$. **Sample 2**: $2$ can wipe out $\{6,19,7\}$, $5$ can wipe out $\{5,15\}$, and $10$ can wipe out $\{10\}$. So for intervals $[1,6]$ and $[1,4]$, you can use all “original numbers” to wipe out everything. For interval $[4,6]$, you can use $2,5$ to wipe out everything. #### Constraints: For $30\%$ of the testdata: $n\le100,m\leq10, d=2, q\le 10$. For $100\%$ of the testdata: $n\le5\times 10^{5},m\leq60,2\leq d\leq10,q\le10^{6},0\le a_i,b_i< 2^{63}$.  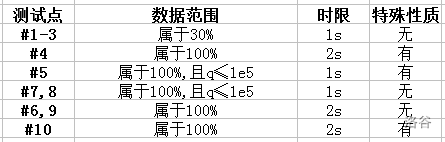Special property: the testdata is constructed. Translated by ChatGPT 5