P5630 [AFOI-19] Power Outage

After the meetup, it was already night. IY and SY were slacking off in the computer lab, writing code templates. Then the lab’s power tripped. Then their “kind” IT teacher told them to fix the breaker. IY and SY, forced by threats, had to fix it. So the following scene happened.

IY and SY found that the main breaker circuit was completely damaged, so they had to rebuild a circuit. There are $n$ current-conducting nodes in the lab. Each node can be connected to other nodes by wires. **Nodes that are connected can transmit current to each other.** Because of reserved-space limitations, some nodes cannot be connected directly. Now IY and SY know there are $m$ pairs of nodes that can be connected directly, and they also know the wire length needed to connect each pair. Having only conducting nodes is not enough. SY took out her long-kept power generator. The generator can be attached to a node and supply power to that node. However, the generator has some limitations: **it can only be attached to node $s$, and it has only $k$ ports, meaning the attached node can connect to at most $k$ wires**. Also, due to linkage effects, **the generator will supply power only if all its ports are connected to wires**. **IY and SY’s goal is to make every node receive power.** They need wires, but the longer the wire, the price grows exponentially. **So they want to make the longest wire as short as possible.** SY is responsible for laying the wires, and IY is assigned to buy the wires, **so he needs to know the total length of wire he has to buy.** Since SY is busy building the circuit, **IY also has to answer each of SY’s queries: what is the total wire length required to make node $u$ and node $v$ connected.** But IY is too weak and does not know the answers. Please help the weak IY answer these questions. As a reward, this problem will give you full marks.

The first line contains four integers $n, m, k, s$, meaning there are $n$ nodes, $m$ pairs of nodes that can be directly connected, the power generator has $k$ ports, and the generator is attached to node $s$. The next $m$ lines each contain three integers $u, v, w$, meaning $u$ and $v$ can be directly connected by a wire, and the required wire length between them is $w$. The next line contains an integer $q$, meaning SY has $q$ queries. The next $q$ lines each contain two integers $u, v$, meaning SY asks IY: how long a wire (in total) is needed to make node $u$ and node $v$ connected.

Output one integer on the first line, representing the total length of all wires. Then output $q$ lines, each containing one integer, representing the answer to each of SY’s queries. **There may be cases with no solution. If there is no solution, output "can not fix it."**, and output nothing else.

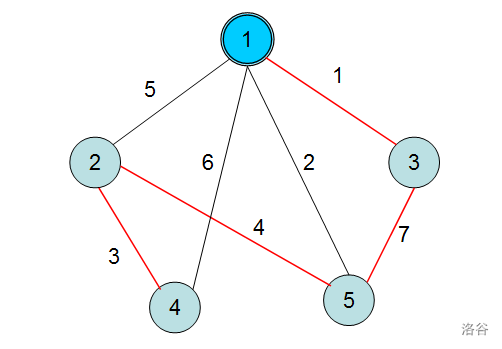
- **Sample Explanation**  As shown, the generator is attached to node $1$ and can connect to only one wire. The red line is the chosen wire. You can see that this is optimal. - **Constraints** For $30\%$ of the testdata: $n \le 10, m \le 30, q \le 10$. For $50\%$ of the testdata: $n \le 2000, m \le 20000, q \le 2000$. For $100\%$ of the testdata: $n \le 30000, m \le 500000, q \le 30000, 1 \le s \le n, 1 \le k \le 150$. For $100\%$ of the testdata: the wire lengths required to connect any two different pairs of nodes are all different (i.e. all edge weights are distinct), and it is guaranteed that no $int$ overflow will occur during computation. - **A Warm Reminder from the Problem Setter** The problem requires making the longest wire as short as possible; on this basis, make the second longest wire as short as possible, and so on. Multiple edges are not ruled out, but the number of edges is sufficient, and no multiple edge will be chosen. It is guaranteed that there are no self-loops, and the data is fully random. Translated by ChatGPT 5