P5638 [CSGRound2] Glory of the Light Steed Rider.

 Little K is daydreaming again. He enters his fantasy world and finds that he has conquered a vast land.

The land that Little K has conquered contains a total of $n$ cities. City $i$ and city $i+1$ are connected by a two-way highway, and traveling along this road takes time $a_i$. In order to care about the people’s lives, Little K decides to make regular visits. Each time, he will travel from city $1$ to city $n$ and visit the cities he passes through. The destination must be city $n$. Moreover, he has a teleporter with teleport radius $k$, meaning he can teleport to $i-k$ and $i+k$. If the target city index is less than $1$, it becomes $1$; if it is greater than $n$, it becomes $n$. However, his teleporter does not have enough power and can only be used once. Also, for some reason, he wants to finish the visits as quickly as possible, so he asks you, the Minister of Transportation, what the minimum time is. Note: **He does not need to visit all cities, and using the teleporter costs no time**.

Two lines. The first line contains two positive integers $n, k$. The second line contains $n-1$ integers, where the $i$-th one denotes $a_i$.

One integer, indicating the answer.

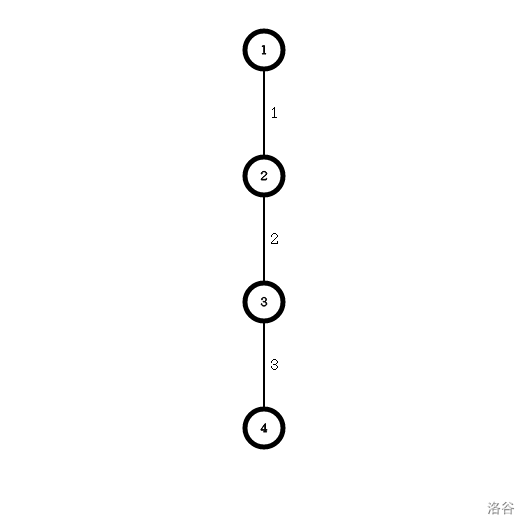
### Sample Explanation 1: The illustrations for samples 1 and 2 are both the following image:  If the teleporter is not used and you just walk directly, the answer is $6$. It can be proven that this is the minimum. ### Sample Explanation 2: Use it at $3$ and teleport to $4$. The answer is $3$. It can be proven that this is the minimum. ### Constraints: For all testdata, $n \ge 2$, $k \ge 1$, $a_i > 0$. | Test Point ID | Range of $n$ | Range of $k$ | Range of $a_i$ | |:-:|:-:|:-:|:-:| | $1 \sim 10$ | $\le 100$ | $\le 100$ | $\le 10^5$ | | $11 \sim 20$ | $\le 3 \times 10^3$ | $\le 3 \times 10^3$ | $\le 10^9$ | | $21$ | $\le 10^5$ | $\le 10^5$ | $\le 10^{12}$ | | $22$ | $\le 2 \times 10^5$ | $\le 2 \times 10^5$ | $\le 10^{12}$ | | $23$ | $\le 5 \times 10^5$ | $\le 5 \times 10^5$ | $\le 10^{12}$ | | $24 \sim 25$ | $\le 10^6$ | $\le 10^6$ | $\le 10^{12}$ | Translated by ChatGPT 5