P5647 ygg发神威

ygg 发神威了，机房的萌新们瑟瑟发抖。

ygg 的机房内共有 $n$ 台电脑且都被使用，为了节省机房内电脑的开销，第 $i$ 台电脑会同时被 $a_i$ 个萌新使用。每台电脑都装有一个「多人在线交流平台」，一台电脑会直接地或间接地通过这个平台与其他所有电脑连接。由于「多人在线交流平台」仍然处于测试阶段，如果一台电脑有多于一种不同的消息传输方式将消息传输到另外的任意一台电脑，就会有各种稀奇古怪的问题产生。两种消息的传输方式被认为是不同的，当且仅当传输消息所经过的直接连接的线路的集合不同，或者传输所经过的电脑的集合不同。当然，消息的传输肯定不会经过一条线路多次。为了避免这种状况，「多人在线交流平台」的线路被特殊地设计了，以使得任意两台电脑之间的传输线路唯一。同时，为了防止一台电脑负荷过大，一台电脑最多会通过「多人在线交流平台」的线路与 $p$ 台电脑相连。 原本两台通过「多人在线交流平台」的线路相连的电脑之间可以相互传输数据，可是 ygg 发现，这会允许使用两台电脑的萌新们互相发送消息，引起大规模~~考试作弊~~膜拜 ygg 的行为。所以他大发神威，切断了所有连接线路的一半。具体地，他将原本通过「多人在线交流平台」的双向线路连接的两台电脑之间的线路变成了单向线路。即，原本通过一条双向线路连接的两台电脑中，只能有一台电脑向另一台电脑发送消息，而另一台电脑不能将任何消息发送回来。 机房内的萌新们在每个时刻都有若干条消息需要传递。如果一台电脑 $i$ 能够直接或间接地通过「多人在线交流平台」的线路连接到电脑 $j$，那么使用电脑 $i$ 的 $a_i$ 个萌新中的任何一个都可以向使用电脑 $j$ 的 $a_j$ 个萌新发送消息。显然，使用同一台电脑的萌新之间的消息只需要在线下传达，不需要使用「多人在线交流平台」，因此不会计入线上发送的消息。 其实机房中的萌新们早已知道了「多人在线交流平台」的管理员密码，所以能够对其线路的连接方向做出修改。可无论他们怎么尝试，都不能恢复最开始时双向连接的状态了。机房中的萌新们当然希望能够尽可能地发送消息，所以他们想要知道，在机房的电脑仅被单向的线路连接时，每一时刻最多能有多少条消息被通过「多人在线交流平台」发送。 为了简化问题，我们假设机房内的所有萌新均能够在同一时刻发送线上消息，并且每一个萌新可以同时向多个人发送消息。 **简要题面：给一棵结点编号** $1\sim n$**，结点权值** $a_i$**，且结点度数最大为** $p$ **的树。求将树的每条边改为有向边后下式的最大值：** $$\sum_{i=1}^{n}\sum_{j=1}^{n}a_ia_j\left[i\rightarrow j\right]$$ $\left[i\rightarrow j\right]$ **定义为：若编号为** $i$ **的结点能通过有向边到达编号为** $j$ **的结点，则值为** $1$**；否则值为** $0$**，且** $\left[i\rightarrow i\right]=0$**。**

输入共 $(n+1)$ 行。 第一行两个正整数 $n$ 和 $p$，分别代表机房内的电脑数与所有电脑的负荷的最大值。 第二行共 $n$ 个正整数，第 $i$ 个整数 $a_i$ 为使用第 $i$ 台电脑的萌新的数量。 接下来 $(n-1)$ 行，第 $(i+2)$ 行两个整数 $u_i,v_i$ ，表示第 $u_i$ 和 $v_i$ 台电脑之间原本有一条「多人在线交流平台」的双向线路。

输出一行一个整数，表示在某一时刻能够发送的消息数的最大值。

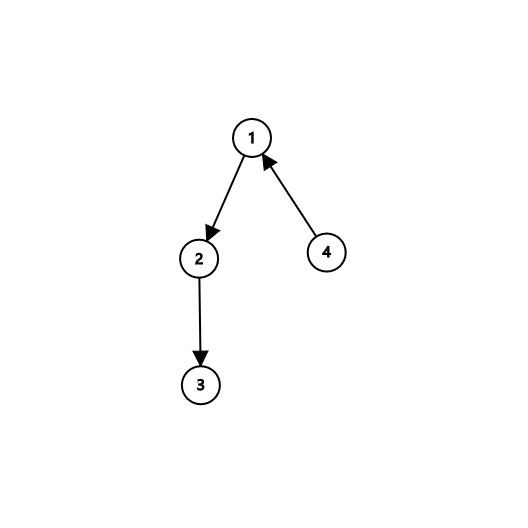
### 样例解释 能够发送的消息最多时的消息传递方向如下：  在该连接方式下发送消息最多的时刻，使用 $1$ 号电脑的 $1$ 个萌新向 $5$ 个萌新各发送了一条消息，共 $1\times5=5$ 条消息； 使用 $2$ 号电脑的 $2$ 个萌新分别向 $3$ 个萌新各发送了一条消息，共 $2\times3=6$ 条消息； 使用 $3$ 号电脑的 $3$ 个萌新不能向任何萌新发送线上消息，因此没有消息从该电脑发送； 使用 $4$ 号电脑的 $4$ 个萌新分别向 $6$ 个萌新各发送了一条消息，共 $4\times6=24$ 条消息。 因此，在某一时刻，最多可以有 $5+6+24=35$ 条线上消息被发送。 可以使用枚举法验证，不存在一种单向的连接方式，使得在某一时刻发送的线上消息的数量能够达到 $36$ 条或更多。 ### 数据范围及约定 对于 $10\%$ 的数据，$n\le10$； 对于另外 $10\%$ 的数据，$n=p+1$； 对于另外 $10\%$ 的数据，$p=2$； 对于另外 $10\%$ 的数据，$p\le20$； 对于另外 $10\%$ 的数据，$p\le40$； 对于所有数据，$2\le n\le10^5$，$2\le p\le50$，$1\le a_i\le100$，$1\le u_i,v_i\le n$。保证给出的双向连接线路能够使任意两台电脑之间的消息传输线路唯一。保证至少有一台电脑原本通过「多人在线交流平台」连接的线路数恰好为 $p$，且没有电脑原本连接的线路数大于 $p$。