P5647 ygg Shows His Power.

ygg shows his power, and the newbies in the computer room are trembling with fear.

There are $n$ computers in ygg's computer room, and all of them are in use. To reduce the cost of computers in the room, the $i$-th computer is used by $a_i$ newbies at the same time. Each computer has an "online multi-user communication platform" installed. Through this platform, every computer is directly or indirectly connected to all other computers. Since the platform is still in the testing stage, if there is more than one different way to transmit a message from one computer to any other computer, various strange problems will occur. Two message transmission methods are considered different if and only if the set of directly connected links used during transmission is different, or the set of computers passed through is different. Of course, a message transmission will never pass through the same link more than once. To avoid this, the platform links are specially designed so that the transmission route between any two computers is unique. Also, to prevent a computer from being overloaded, each computer can be connected to at most $p$ computers via platform links. Originally, two computers connected by a platform link could transmit data to each other. But ygg found that this would allow newbies using the two computers to send messages to each other, causing large-scale ~~exam cheating~~ worshipping ygg. So he showed his power and cut off half of all links. Specifically, he changed each original bidirectional link between two computers into a unidirectional link. That is, between two computers originally connected by one bidirectional link, only one computer can send messages to the other, and the other cannot send any message back. At every moment, the newbies in the computer room have some messages to transmit. If computer $i$ can directly or indirectly reach computer $j$ through the platform links, then any of the $a_i$ newbies using computer $i$ can send messages to the $a_j$ newbies using computer $j$. Clearly, messages between newbies using the same computer can be delivered offline and do not need the platform, so they are not counted as online messages. In fact, the newbies already know the administrator password of the platform, so they can change the directions of the links. However, no matter how they try, they can no longer restore the original bidirectional state. The newbies of course hope to send as many messages as possible, so they want to know: when the computers are connected only by directed links, what is the maximum number of messages that can be sent through the platform at any moment. To simplify the problem, assume that all newbies can send online messages at the same time, and each newbie can send messages to multiple people simultaneously. **Brief statement: Given a tree with nodes numbered** $1\sim n$**, node weights** $a_i$**, and maximum node degree** $p$**. After changing every edge of the tree into a directed edge, find the maximum value of the following expression:** $$\sum_{i=1}^{n}\sum_{j=1}^{n}a_ia_j\left[i\rightarrow j\right]$$ $\left[i\rightarrow j\right]$ **is defined as follows: if the node numbered** $i$ **can reach the node numbered** $j$ **through directed edges, then it equals** $1$**; otherwise it equals** $0$**, and** $\left[i\rightarrow i\right]=0$**.**

The input has $(n+1)$ lines. The first line contains two positive integers $n$ and $p$, representing the number of computers in the computer room and the maximum load limit of all computers. The second line contains $n$ positive integers. The $i$-th integer $a_i$ is the number of newbies using the $i$-th computer. The next $(n-1)$ lines each contain two integers $u_i,v_i$, indicating that there was originally a bidirectional link of the "online multi-user communication platform" between computer $u_i$ and computer $v_i$.

Output one line with one integer, representing the maximum number of messages that can be sent at a moment.

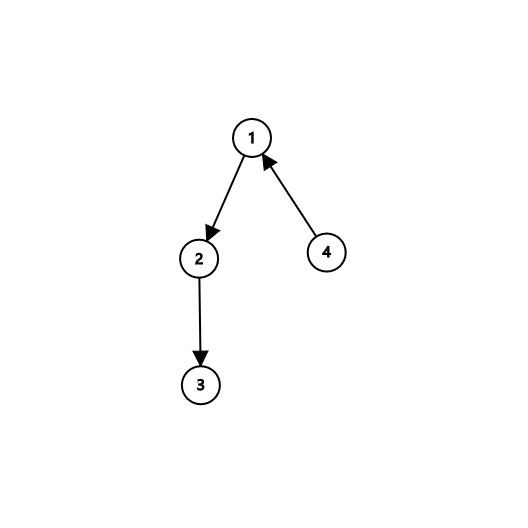
### Sample Explanation When the number of messages that can be sent is maximized, the directions of message transmission are as follows:  At the moment when this connection method sends the most messages: the $1$ newbie using computer $1$ sends one message to each of $5$ newbies, for a total of $1\times5=5$ messages; the $2$ newbies using computer $2$ each send one message to each of $3$ newbies, for a total of $2\times3=6$ messages; the $3$ newbies using computer $3$ cannot send any online messages, so no messages are sent from this computer; the $4$ newbies using computer $4$ each send one message to each of $6$ newbies, for a total of $4\times6=24$ messages. Therefore, at a certain moment, at most $5+6+24=35$ online messages can be sent. You can verify by enumeration that there is no directed connection method that can make the number of online messages sent at a moment reach $36$ or more. ### Constraints and Notes For $10\%$ of the data, $n\le10$. For another $10\%$ of the data, $n=p+1$. For another $10\%$ of the data, $p=2$. For another $10\%$ of the data, $p\le20$. For another $10\%$ of the data, $p\le40$. For all data, $2\le n\le10^5$, $2\le p\le50$, $1\le a_i\le100$, $1\le u_i,v_i\le n$. It is guaranteed that the given bidirectional links make the message transmission route between any two computers unique. It is guaranteed that at least one computer originally has exactly $p$ platform links, and no computer originally has more than $p$ platform links. Translated by ChatGPT 5