P5658 [CSP-S 2019] Bracket Tree

In this problem, a **valid bracket sequence** is defined as follows: 1. `()` is a valid bracket sequence. 2. If `A` is a valid bracket sequence, then `(A)` is a valid bracket sequence. 3. If `A` and `B` are valid bracket sequences, then `AB` is a valid bracket sequence. In this problem, the definitions of a **substring** and **distinct substrings** are as follows: 1. A substring of a string `S` is a string formed by any **continuous** characters in `S`. A substring of `S` can be represented by the starting position $l$ and the ending position $r$, denoted as $S (l, r)$ ($1 \leq l \leq r \leq |S |$, where $|S |$ denotes the length of `S`). 2. Two substrings of `S` are considered different **if and only if** their positions in `S` are different, i.e. $l$ is different or $r$ is different.

A tree of size $n$ contains $n$ nodes and $n - 1$ edges. Each edge connects two nodes, and between any two nodes there exists **exactly one** simple path. Xiao Q is a curious kid. One day on his way to school, he encountered a tree of size $n$. The nodes of the tree are numbered from $1 \sim n$, and node $1$ is the root. Except for node $1$, every node has a parent node. The parent of node $u$ ($2 \leq u \leq n$) is node $f_u$ ($1 \le f_u < u$). Xiao Q found that each node of the tree has **exactly** one bracket, either `(` or `)`. Xiao Q defines $s_i$ as follows: take the brackets on the simple path from the root to node $i$, and arrange them into a string in the order the nodes are visited. Obviously, $s_i$ is a bracket string, but it is not necessarily a valid bracket sequence. Now Xiao Q wants, for all $i$ ($1 \leq i \leq n$), to find how many **distinct substrings** of $s_i$ are **valid bracket sequences**. This problem stumped Xiao Q, so he asks you for help. Suppose $s_i$ has $k_i$ distinct substrings that are valid bracket sequences. You only need to tell Xiao Q the XOR sum of all $i \times k_i$, namely: $$ (1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n) $$ where $\text{xor}$ is the bitwise XOR operation.

The first line contains an integer $n$, denoting the size of the tree. The second line contains a bracket string of length $n$ consisting of `(` and `)`. The $i$-th bracket denotes the bracket on node $i$. The third line contains $n − 1$ integers. The $i$-th integer ($1 \leq i \lt n$) denotes the parent index $f_{i+1}$ of node $i + 1$.

Only one line containing one integer, denoting the answer.

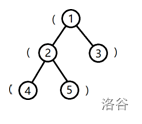
**[Sample 1 Explanation]** The shape of the tree is shown in the figure below:  The string formed by the brackets on the simple path from the root to node 1, arranged in order, is `(`, and the number of substrings that are valid bracket sequences is $0$. The string from the root to node 2 is `((`, and the number of substrings that are valid bracket sequences is $0$. The string from the root to node 3 is `()`, and the number of substrings that are valid bracket sequences is $1$. The string from the root to node 4 is `(((`, and the number of substrings that are valid bracket sequences is $0$. The string from the root to node 5 is `(()`, and the number of substrings that are valid bracket sequences is $1$. **[Sample 2]** See `brackets/brackets2.in` and `brackets/brackets2.ans` under the contestant directory. **[Constraints]** ::cute-table{tuack} | Test Point ID | $n\le$ | Special Property | |:-:|:-:|:-:| | $1\sim 2$ | $8$ | $f_i=i-1$ | | $3\sim 4$ | $200$ | ^ | | $5\sim 7$ | $2000$ | ^ | | $8\sim 10$ | ^ | None | | $11\sim 14$ | $10^5$ | $f_i=i-1$ | | $15\sim 16$ | ^ | None | | $17\sim 20$ | $5\times 10^5$ | ^ | Translated by ChatGPT 5