P5663 [CSP-J 2019] Processing Parts

Kaikai’s factory is producing a magical part in an orderly way, and of course the production process is also magical. There are $n$ workers in the factory, numbered from $1 \sim n$. Between some pairs of workers, there are two-way conveyor belts for transporting parts. It is guaranteed that there is at most one conveyor belt between any two workers. If worker $x$ wants to produce a part processed to stage $L\,(L \gt 1)$, then **all** workers that are **directly** connected to worker $x$ by a conveyor belt need to produce a part processed to stage $L - 1$ (but worker $x$ himself/herself does **not** need to produce a stage $L - 1$ part). If worker $x$ wants to produce a part processed to stage $1$, then **all** workers that are **directly** connected to worker $x$ by a conveyor belt need to provide worker $x$ with one raw material. Xuanxuan is worker $1$. Now $q$ work orders are given. The $i$-th work order means that the worker numbered $a_i$ wants to produce a part at stage $L_i$. For each work order, Xuanxuan wants to know whether he needs to provide raw materials for others. He knows that smart you can help him compute it.

The first line contains three positive integers $n$, $m$, and $q$, representing the number of workers, the number of conveyor belts, and the number of work orders. The next $m$ lines each contain two positive integers $u$ and $v$, indicating that there is a conveyor belt between worker $u$ and worker $v$. It is guaranteed that $u \neq v$. The next $q$ lines each contain two positive integers $a$ and $L$, indicating that worker $a$ wants to produce a part at stage $L$.

Output $q$ lines, each containing a string `Yes` or `No`. If producing according to the $i$-th work order requires Xuanxuan (worker $1$) to provide raw materials, output `Yes` on the $i$-th line; otherwise output `No`.

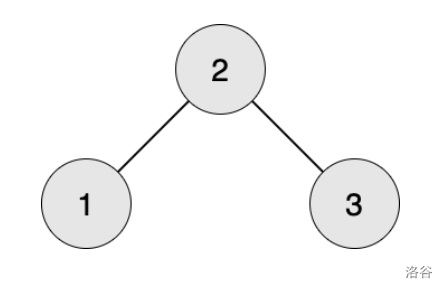
**Sample 1 Explanation**  If worker $1$ wants to produce a stage $1$ part, worker $2$ needs to provide raw materials. If worker $2$ wants to produce a stage $1$ part, workers $1$ and $3$ need to provide raw materials. If worker $3$ wants to produce a stage $1$ part, worker $2$ needs to provide raw materials. If worker $1$ wants to produce a stage $2$ part, worker $2$ needs to produce a stage $1$ part, and workers $1$ and $3$ need to provide raw materials. If worker $2$ wants to produce a stage $2$ part, workers $1$ and $3$ need to produce a stage $1$ part, and both of them need worker $2$ to provide raw materials. If worker $3$ wants to produce a stage $2$ part, worker $2$ needs to produce a stage $1$ part, and workers $1$ and $3$ need to provide raw materials. 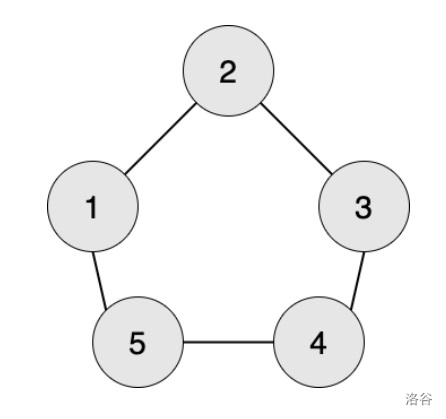**Sample 2 Explanation**  If worker $1$ wants to produce a stage $1$ part, workers $2$ and $5$ need to provide raw materials. If worker $1$ wants to produce a stage $2$ part, workers $2$ and $5$ need to produce a stage $1$ part, and workers $1,3,4$ need to provide raw materials. If worker $1$ wants to produce a stage $3$ part, workers $2$ and $5$ need to produce a stage $2$ part, workers $1,3,4$ need to produce a stage $1$ part, and workers $2,3,4,5$ need to provide raw materials. If worker $1$ wants to produce a stage $4$ part, workers $2$ and $5$ need to produce a stage $3$ part, workers $1,3,4$ need to produce a stage $2$ part, workers $2,3,4,5$ need to produce a stage $1$ part, and all workers need to provide raw materials. If worker $1$ wants to produce a stage $5$ part, workers $2$ and $5$ need to produce a stage $4$ part, workers $1,3,4$ need to produce a stage $3$ part, workers $2,3,4,5$ need to produce a stage $2$ part, all workers need to produce a stage $1$ part, and all workers need to provide raw materials. **Constraints** There are $20$ test points in total. For all test points, it is guaranteed that $1 \leq u, v, a \leq n$. For test points $1\sim4$, $1 \leq n, m \leq 1000$, $q = 3$, $L = 1$. For test points $5\sim8$, $1 \leq n, m \leq 1000$, $q = 3$, $1 \leq L \leq 10$. For test points $9\sim12$, $1 \leq n, m, L \leq 1000$, $1 \leq q \leq 100$. For test points $13\sim16$, $1 \leq n, m, L \leq 1000$, $1 \leq q \leq 10^5$. For test points $17\sim20$, $1 \leq n, m, q \leq 10^5$, $1 \leq L \leq 10^9$. Translated by ChatGPT 5