P5671 "SWTR-2" Triangles

Little $\mathrm{A}$ is learning math.

He encountered two puzzles: - In a plane, the **line segment** $DE$ intersects the **line** $FG$ at point $O$. Given $\angle DOF=x^{\circ}$, find a point $P$ on the **line** $FG$ such that $\triangle DOP$ is an **isosceles** triangle, and compute the measure of $\angle D$. (If the answer is not an integer, keep $1$ decimal place.) - Given a **right triangle** with two sides $m,n$, find the length of the third side (keep $5$ decimal places).  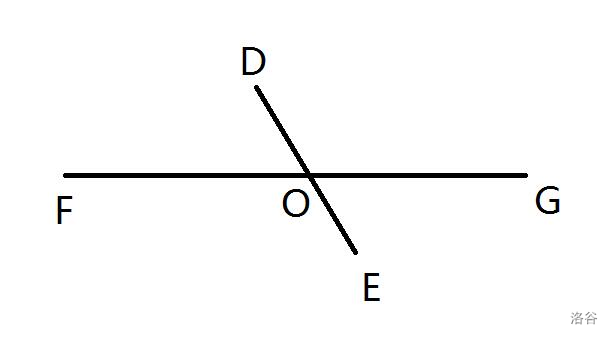Write a program to compute the answers to the problems.

One line with three **positive integers**: $x,m,n$.

Output two lines. The first line is the answer to the first question, and the second line is the answer to the second question. If there are multiple solutions, separate them with **spaces** and output them in **increasing** order.

--- ### Sample Explanation Problem $1$: - When point $P$ is to the left of point $O$, the formed $\triangle DOP$ is an equilateral triangle, so $\angle D=60^{\circ}$. - When point $P$ is to the right of point $O$, in the formed $\triangle DOP$, $\angle DOP=180^{\circ}-60^{\circ}=120^{\circ}$ is the vertex angle, so $\angle D=(180^{\circ}-120^{\circ})/2=30^{\circ}$. Problem $2$: The third side is the hypotenuse, with length $\sqrt{1^2+1^2}=\sqrt{2}=1.41421\dots$. --- ### Constraints and Notes $x