P5674 「SWTR-2」Magical Gates
题目背景
小 $\mathrm{A}$ 找到了一张藏宝图。
他顺着藏宝图上的路线来到了一扇古老的大门前,门上有六芒星的图案。
他把手轻轻地放在六芒星上……
霎时间,六芒星光芒大放,四周亮如白昼。
(新增一组大样例)
题目描述
小 $\mathrm{A}$ 面前出现了 $10^{1000}$ 扇门,每个门上都写着它自己的编号,分别为 $1,2,3,\dots,10^{1000}$。
这时,守门人小 $\mathrm{M}$ 向小 $\mathrm{A}$ 走来。
“这些门,并不普通,它有魔力。”
“我会给你一些区间 $l,r$,请你求出区间 $[l,r]$ 里所有门的魔力值之**和**与魔力值之**积**。”
“因为结果可能很大,请你将结果 $mod\ p$。 ”
“如果你正确地回答了所有询问,你将会拥有这扇门后的所有宝藏。”
“哦,对了,一扇门的魔力值就是其在二进制下 $1$ 的个数。”
简单来说,记第 $i$ 扇门的魔力值为 $d_i$,给定的区间为 $[l,r]$,请求出:
$$\sum_{l}^{r}d_i\bmod\ p \quad \prod_{l}^{r}d_i\bmod\ p$$
由于门的数量实在太多,小 $\mathrm{A}$ 决定向你请求帮助。
输入格式
第一行三个正整数 $T,p,n$($n$ 会在数据范围中说明)。
接下来 $T$ 行,第 $i$ 行两个**正整数** $l_i,r_i$。
输出格式
输出 $T$ 行,每行 $2$ 个数,由空格隔开,第 $i$ 行分别为:
$$\sum_{l}^{r}d_i\bmod\ p \quad \prod_{l}^{r}d_i\bmod\ p$$
说明/提示
---
### 样例说明
数据 $1$:
$$\sum_{3}^{7}d_i=2+1+2+2+3=10$$
$$\prod_{3}^{7}d_i=2\times 1\times 2\times 2\times 3=24$$
数据 $2$:
$$\sum_{1}^{10}d_i=1+1+2+1+2+2+3+1+2+2=17$$
$$\prod_{1}^{10}d_i=1\times 1\times 2\times 1\times 2\times 2\times 3\times 1\times 2\times 2=96$$
---
### 数据范围与约定
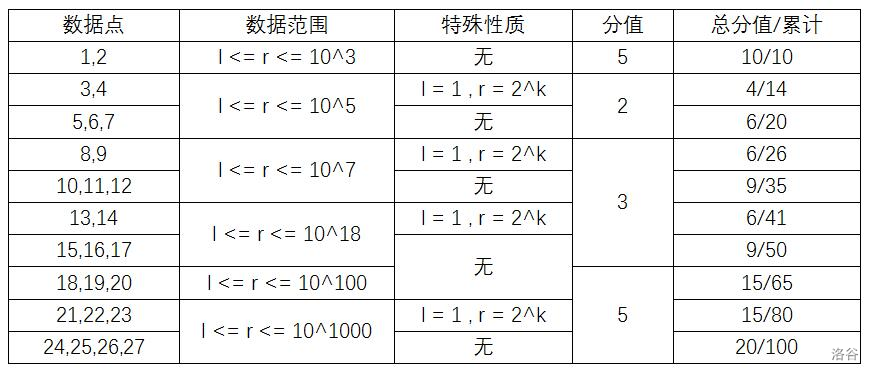
为了方便拿部分分,输入格式中的 $n$ 为**该测试点的编号**。
所有具有特殊性质的测试点一共 $31\%$。
对于 $100\%$ 的数据,有 $1\leq n\leq 27,1\leq T \leq 10,10^9 \leq p \leq 1.001\times 10^9,1\leq l\leq r\leq 10^{1000}$,**保证 $p$ 为质数**。
---
对于测试点 $1-20$,时限 $300ms$,剩下的 $7$ 个测试点时限 $2s$。
对于所有测试点,空间限制 $256MB$
---
“吱嘎”一声,封尘千年的大门缓缓打开。
刺眼的金光照了出来……