P5674 "SWTR-2" Magical Gates

Little $\mathrm{A}$ found a treasure map. Following the route on the map, he arrived at an ancient gate with a hexagram pattern on it. He gently placed his hand on the hexagram... In an instant, the hexagram shone brightly, and the surroundings became as bright as day. (One new large sample has been added.)

In front of Little $\mathrm{A}$ appeared $10^{1000}$ gates. Each gate has its own index written on it, namely $1,2,3,\dots,10^{1000}$. At this moment, the gatekeeper Little $\mathrm{M}$ walked up to Little $\mathrm{A}$. "These gates are not ordinary. They have magic." "I will give you some intervals $l,r$. Please find the **sum** and the **product** of the magic values of all gates in the interval $[l,r]$." "Since the result may be very large, output the result $mod\ p$." "If you answer all queries correctly, you will own all the treasure behind this gate." "Oh, right. The magic value of a gate is the number of $1$ bits in its binary representation." In short, let the magic value of the $i$-th gate be $d_i$. Given an interval $[l,r]$, compute: $$\sum_{l}^{r}d_i\bmod\ p \quad \prod_{l}^{r}d_i\bmod\ p$$ Because there are far too many gates, Little $\mathrm{A}$ decided to ask you for help.

The first line contains three positive integers $T,p,n$ ($n$ will be explained in Constraints). The next $T$ lines: on the $i$-th line there are two **positive integers** $l_i,r_i$.

Output $T$ lines. Each line contains $2$ numbers separated by a space. The $i$-th line should be: $$\sum_{l}^{r}d_i\bmod\ p \quad \prod_{l}^{r}d_i\bmod\ p$$

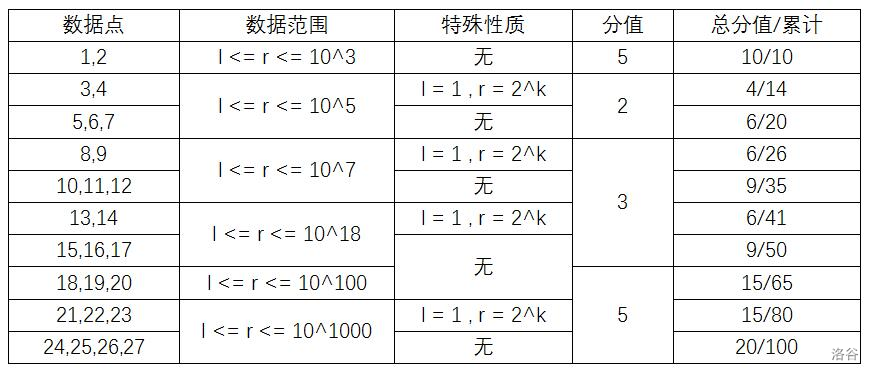
--- ### Sample Explanation Testdata 1: $$\sum_{3}^{7}d_i=2+1+2+2+3=10$$ $$\prod_{3}^{7}d_i=2\times 1\times 2\times 2\times 3=24$$ Testdata 2: $$\sum_{1}^{10}d_i=1+1+2+1+2+2+3+1+2+2=17$$ $$\prod_{1}^{10}d_i=1\times 1\times 2\times 1\times 2\times 2\times 3\times 1\times 2\times 2=96$$ --- ### Constraints and Notes  To make it easier to get partial scores, the $n$ in the input format is the **index of the current test point**. All test points with special properties take up a total of $31\%$. For $100\%$ of the data, $1\leq n\leq 27,1\leq T \leq 10,10^9 \leq p \leq 1.001\times 10^9,1\leq l\leq r\leq 10^{1000}$, and **$p$ is guaranteed to be prime**. --- For test points $1-20$, the time limit is $300ms$, and for the remaining $7$ test points the time limit is $2s$. For all test points, the memory limit is $256MB$. --- With a "creak", the dust-covered gate that had been sealed for a thousand years slowly opened. A dazzling golden light shone out... Translated by ChatGPT 5