[GZOI2017] 小z玩游戏
题目背景
GZOI2017 D1T2
题目描述
小 z 很无聊。
小 z 要玩游戏。
小 z 有 $N$ 个新游戏，第 $i$ 个游戏看上去的有趣程度为 $w_i$。
小 z 很挑，他只会玩看上去的有趣程度是自己兴奋程度整数倍的游戏。
由于游戏实际上有好玩的也有不好玩的，玩完第 $i$ 个游戏后，小 z 的兴奋程度会变为 $e_i$。
已知小 z 初始兴奋程度为 $1$，请问小 z 有多少个游戏可能会玩两次？
输入输出格式
输入格式
第一行一个正整数 $T$，表示测试数据组数，最多 $10$ 组。
对于每组测试数据：
- 第一行一个正整数 $N$，表示游戏的个数。
- 第二行 $N$ 个正整数，第 $i$ 个数 $w_i$，表示第 $i$ 个游戏看上去的有趣程度为 $w_i$。
- 第三行 $N$ 个正整数，第 $i$ 个数 $e_i$，表示小 z 玩完第 $i$ 个游戏后，小 z 的兴奋程度会变为 $e_i$。
输出格式
共 $T$ 行。
每行一个正整数，表示对应测试数据，小 z 可能会玩两次的游戏数量。
输入输出样例
输入样例 #1
5
1
100000
100000
5
1 2 6 15 35
5 7 9 2 3
5
2 3 5 35 21
7 11 7 3 2
10
6 15 77 12 24 37 35 99 55 42
4 2 5 7 11 3 6 8 9 10
10
6540 5604 567 57065 60 670 6870 1230 465 6540
12 5 37 3 34 13 17 18 10 12输出样例 #1
1
3
3
8
5说明
### 样例 2 解释
数字代表游戏编号，箭头表示下一个。
- 情况 $1$：$2\to 5\to 4\to 2$；
- 情况 $2$：$5\to 4\to 2\to 5$；
- 情况 $3$：$4\to 2\to 5\to 4$。
所以小 z 可能玩 $2,4,5$ 两次。
小 z 无论如何都不能玩 $1$ 或 $3$ 两次。
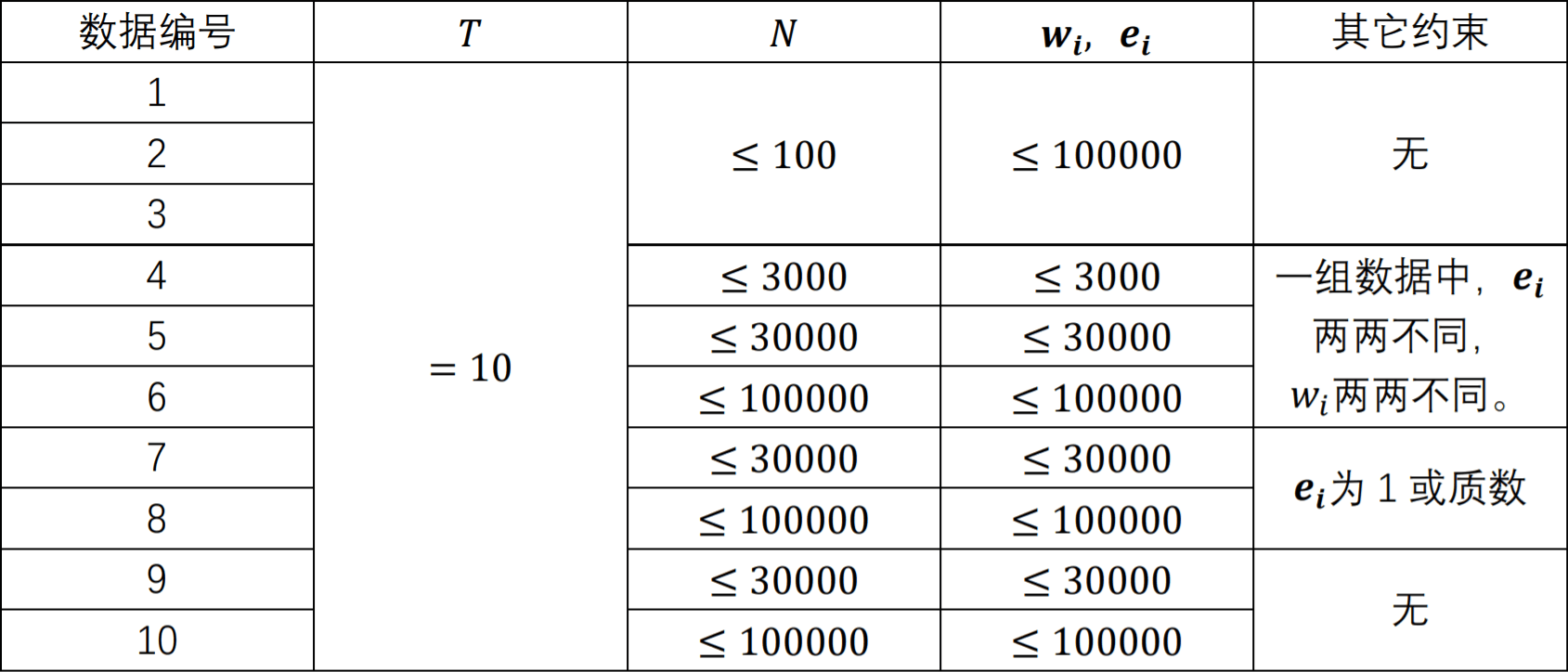
### 数据范围及约定
