P5676 [GZOI2017] Little z Plays Games

GZOI2017 D1T2.

Little z is very bored. Little z wants to play games. Little z has $N$ new games. The apparent fun level of the $i$-th game is $w_i$. Little z is picky. He will only play a game whose apparent fun level is an integer multiple of his excitement level. Since some games are actually fun and some are not, after finishing the $i$-th game, Little z’s excitement level will become $e_i$. It is known that Little z’s initial excitement level is $1$. Please determine how many games Little z might play twice.

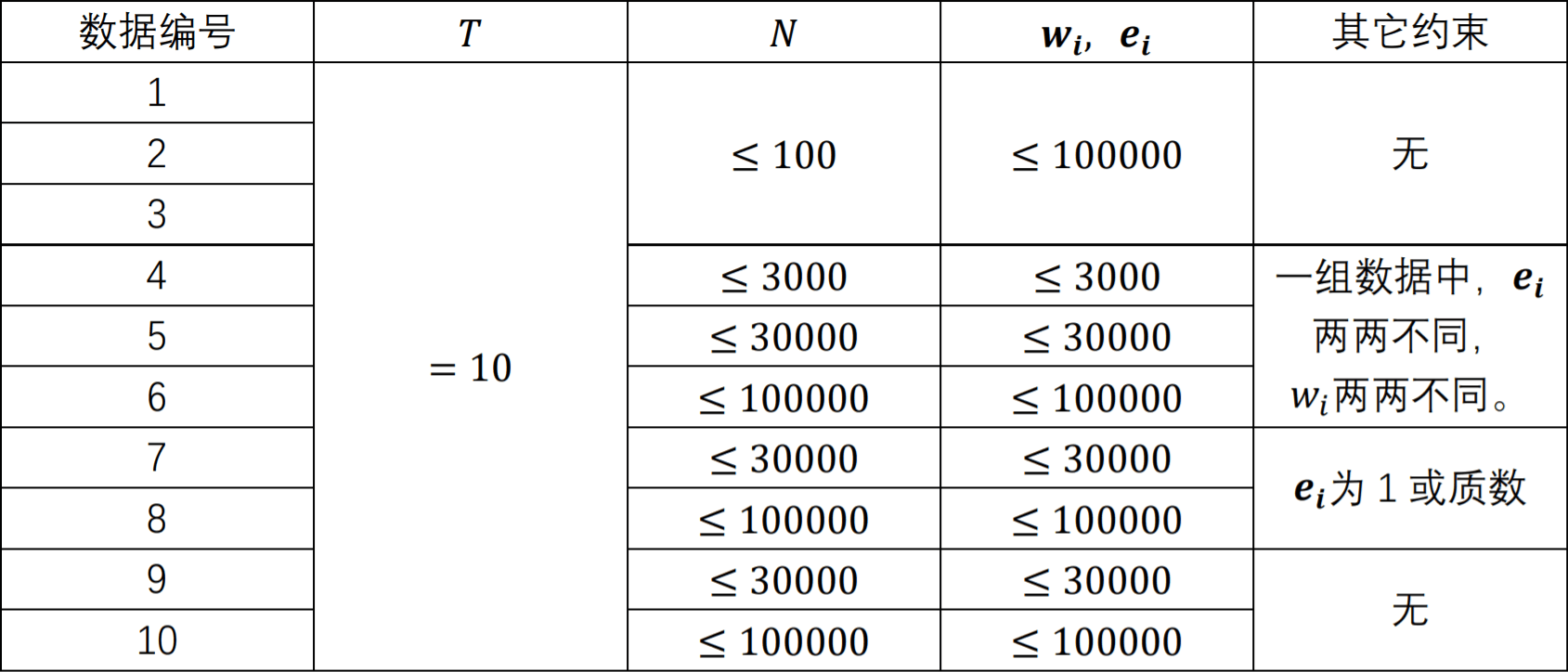
The first line contains a positive integer $T$, indicating the number of testdata groups, up to $10$ groups. For each group of testdata: - The first line contains a positive integer $N$, indicating the number of games. - The second line contains $N$ positive integers. The $i$-th number $w_i$ indicates that the apparent fun level of the $i$-th game is $w_i$. - The third line contains $N$ positive integers. The $i$-th number $e_i$ indicates that after Little z finishes the $i$-th game, his excitement level will become $e_i$.

Output $T$ lines in total. Each line contains one positive integer, indicating for the corresponding testdata group, the number of games that Little z might play twice.

### Explanation for Sample 2 Numbers represent game indices, and arrows indicate the next one. - Case $1$: $2\to 5\to 4\to 2$. - Case $2$: $5\to 4\to 2\to 5$. - Case $3$: $4\to 2\to 5\to 4$. So Little z might play games $2,4,5$ twice. No matter what, Little z cannot play game $1$ or $3$ twice. ### Constraints  Translated by ChatGPT 5