P5677 [GZOI2017] Pairing Statistics

GZOI2017 D1T3

Given $n$ numbers $a_1,\cdots,a_n$. For a pair $(x,y)$, if for all $i=1,2,\cdots,n$, it satisfies $|a_x-a_y|\le|a_x-a_i|(i\not=x)$, then $(x,y)$ is called a good pair ($|x|$ denotes the absolute value of $x$). You are given several queries. For each query, ask how many good pairs are contained in the interval $[l,r]$. That is, choose $x,y$ ($l\le x,y\le r$ and $x\not=y$), and ask how many pairs $(x,y)$ are good pairs.

The first line contains two positive integers $n,m$. The second line contains $n$ numbers $a_1,\cdots,a_n$. In the next $m$ lines, each line gives two numbers $l,r$.

Let $Ans_i$ be the answer to the $i$-th query. Output $\sum_{i=1}^m\limits Ans_i\times i$.

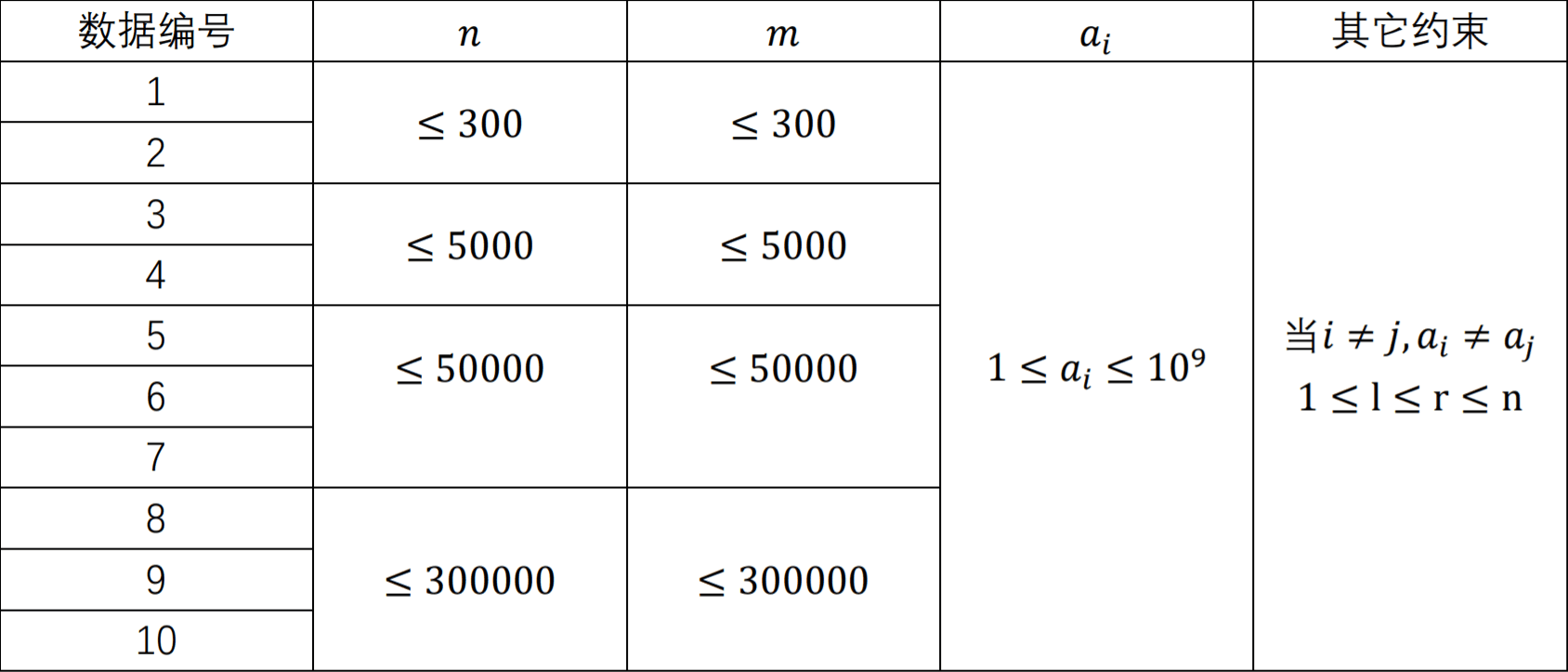
**Sample Explanation** In the first query, the good pairs are: $(1,2)(2,1)$. In the second query, the good pairs are: $(1,2)(2,1),(1,3)(3,1)$. The answer $=2\times 1+4\times 2=10$. **Constraints**  Translated by ChatGPT 5