P5680 [GZOI2017] Shared Bicycles

GZOI2017 D2T3

There are two shared bicycle companies, Company A and Company B, competing on a campus. To increase its market share on campus as much as possible, Company A will try to interfere with Company B’s recycling operations. The whole campus consists of $N$ areas and $M$ roads, where each road connects two areas. There is an area $K$ that is Company B’s base. All recycling operations **start** from this area. To reduce costs, when recycling, for going from area $K$ to any area $X$, Company B always chooses a **shortest** path. If there are multiple shortest paths to some area, it chooses, among all shortest paths, the one whose previous area on the path has the **smallest index**. This path is called the **recycling route** from $K$ to $X$. All **recycling routes** form a tree structure, called the **recycling route tree**. In the figure below, the green edges form a **recycling route tree**.  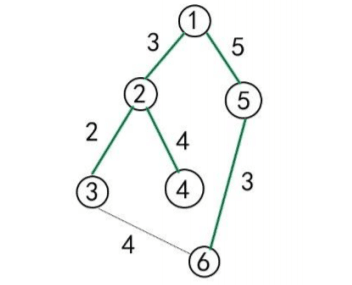Each time, Company B recycles bicycles from several areas; these areas are called **recycling areas**. Company B also designates some areas as **deployment areas**, and the remaining areas are called **non-deployment areas**. On the **recycling route tree**, mark area $K$, mark all **recycling areas**, and also mark the lowest common ancestor on the **recycling route tree** of any two **recycling areas**. In the figure below, suppose areas $4$ and $6$ are **deployment areas**, and areas $4, 5, 6$ are **recycling areas**. Then the marked areas are $1, 4, 5, 6$.  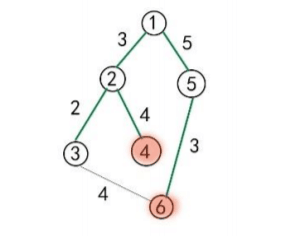Company A interferes with Company B’s recycling operation **if and only if** for every marked **deployment area** $X$ other than $K$, on the **recycling route** from area $K$ to $X$, there exist two marked areas such that **all roads** (the path between the two nodes on the recycling route tree) between them are blocked. The cost to block a road is the length of that road. In the figure above, Company A chooses to block the two paths $1 \rightsquigarrow 4$ and $5 \rightsquigarrow 6$, and the cost is $3+4+3=10$. Your task is to help Company A compute how to block Company B’s recycling operation with the minimum total cost.

The first line contains four integers $N, M, K, Q$, representing the number of areas on campus, the number of roads, the index $K$ of Company B’s base, and the number of operations. Lines $2$ to $M + 1$ describe the roads. Each line contains three integers $S, T, Len$, meaning there is an undirected road of length $Len$ between $S$ and $T$. Then, lines $M + 2$ to $M + Q + 1$ describe the operations. The first integer of each line indicates the operation type: $0$ means Company B changes the **deployment areas**, and $1$ means one recycling operation by Company B. For an operation of type $0$, it is followed by an integer $num$, meaning the number of areas to be changed, and then $num$ integers giving the area indices. For each changed area, if it is a **deployment area**, change it to a **non-deployment area**; if it is a **non-deployment area**, change it to a **deployment area**. For an operation of type $1$, it is followed by an integer $num$, meaning the number of **recycling areas**, and then $num$ integers giving the indices of Company B’s **recycling areas**. Each time, you need to remark nodes on the **recycling route tree**.

For each recycling operation, output one line with the minimum cost for Company A to interfere with Company B. Note that if there is no marked **deployment area**, output $-1$.

【Constraints】 For $30\%$ of the testdata, $N\le 200$, $Q\le 200$. For $60\%$ of the testdata, it is guaranteed that in each operation, the number of **recycling areas** is always $N-1$. For $80\%$ of the testdata, $N\le 20000$, $M=N-1$, $Q\le 1000$, $num\le 200$. For $100\%$ of the testdata, $N\le 50000$, $M\le 100000$, $Q\le 1500$, $num\le 500$. All testdata guarantee that there are no self-loops. All road lengths are less than $2000$, and area $K$ is never a **deployment area** at any time. Translated by ChatGPT 5