P5689 [CSP-S 2019 Jiangxi] D-ary Heap

JXCSP-S T5.

A d-ary heap is a tree-structured data structure. In this problem, we only consider the min-heap, which satisfies that for every node except the root, the weight of the node is not less than the weight of its parent. Except for leaf nodes, every node has at least one child. Initially, there are $n$ nodes, numbered $0 \sim n - 1$. Each node is a single-node tree rooted at itself. Then there are $q$ operations in order, and each operation is one of the following two types: * `1 x y`: Choose nodes $x$ and $y$ that are not in the same tree. Attach the root of the tree containing $x$ directly under the root of the tree containing $y$. Then the trees containing $x$ and $y$ merge into one tree. * `2 x`: Choose a node $x$, and let the number of nodes in the tree containing $x$ be $size$. You need to compute how many different d-ary heaps can be produced by filling the $size$ numbers $0 \sim size - 1$ into the nodes of the tree containing $x$. Two heaps are different if and only if there exists a node whose filled value is different. Since the answer may be very large, you only need to output the result modulo $10^9+7$.

The first line contains two integers $n,q$, whose meanings are described above. In the next $q$ lines, each line is in one of the following formats: * `1 x' y'`: You need to compute $x=(x'+ans) \bmod n , y=(y'+ans) \bmod n$ to get the actual $x$ and $y$. The input guarantees that the trees containing $x$ and $y$ are different. * `2 x'`: You need to compute $x=(x'+ans) \bmod n$ to get the actual $x$. Here, $ans$ denotes the output of the previous type $2$ operation, and initially $ans=0$.

For each type $2$ operation, output one line with one integer representing the answer.

#### Sample 1 Explanation In the 1st operation, attach the root $1$ of the tree containing $1$ under the root $0$ of the tree containing $0$. In the 2nd operation, attach the root $2$ of the tree containing $2$ under the root $0$ of the tree containing $0$. In the 3rd operation, the tree containing $1$ is shown in Figure 1. Filling $0,1,2$ with $[0,1,2]$ and $[0,2,1]$ can produce $2$ different heaps. In the 4th operation, $x=(3+2) \bmod 5=0$, $y=(1+2) \bmod 5=3$. Attach the root $0$ of the tree containing $0$ under the root $3$ of the tree containing $3$. In the 5th operation, $x=(2+2) \bmod 5=4$, $y=(0+2) \bmod 5=2$. Attach the root $4$ of the tree containing $4$ under the root $3$ of the tree containing $2$. In the 6th operation, $x=(4+2) \bmod 5=1$. The tree containing $1$ is shown in Figure 2. Filling $0\sim 4$ with $[1,2,3,0,4]$, $[1,3,2,0,4]$, $[1,2,4,0,3]$, $[1,4,2,0,3]$, $[1,3,4,0,2]$, $[1,4,3,0,2]$, $[2,4,3,0,1]$, $[2,3,4,0,1]$ can produce $8$ different heaps.  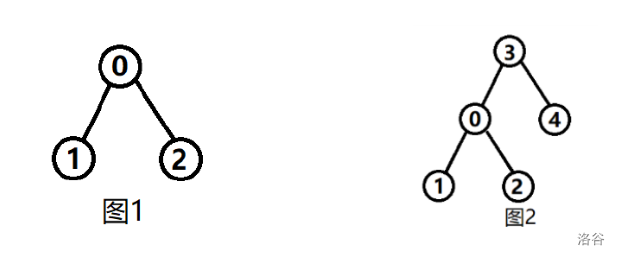#### Constraints and Conventions For $100\%$ of the data, $0\le x',y'