P5696 [CTSC1998] Surveillance Cameras

CTSC1998 D1T2. A famous warehouse management company, SERKOI, asks your company to install a CCTV surveillance system for it. Because SERKOI has limited funds, each room can only have one camera for surveillance, but its lens can rotate in **any direction**.

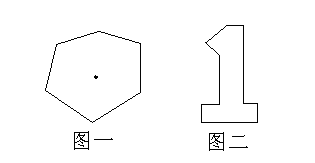
Our task is to determine the camera position so that every corner of the room can be monitored by it. For example, Figure 1 and Figure 2 are sketches of two rooms. Each room is represented by a closed polygon.  Each edge in the figure represents a wall. For the room in Figure 1, placing the camera at the black point meets the requirement. For the room in Figure 2, no matter where the camera is placed, the requirement cannot be met. Write a program that, given a room sketch, determines whether it is possible to place **one** camera somewhere inside the room so that it can monitor **any** corner of the room.

The input contains one or more room descriptions. The first line of each description is a positive integer $n$, indicating that the room sketch is an $n$-gon. The next $n$ lines each contain two integers $x, y$ separated by spaces, which are the coordinates of the $n$ vertices of the polygon in the Cartesian coordinate system, listed in clockwise order. $n = 0$ indicates the end of input.

For each room, first output one line with the room index in the format `Room #k:`, where $k$ starts from $1$ in the input order. The next line is the result. If placing a camera somewhere in the room can satisfy the condition, output `Surveillance is possible.`; otherwise output `Surveillance is impossible.` Print a blank line between the outputs of every two rooms.

Constraints $4 \leq n \leq 100$，$-10000 \leq x, y \leq 10000$。 Translated by ChatGPT 5