P5750 [NOI1999] Nails and Balls

There is a triangular wooden board standing vertically. On it, $\frac{ n (n+1) } { 2 }$ nails are hammered in, and there are $(n+1)$ slots (see Figure 1 when $n=5$). The distance between each nail and its surrounding nails is $d$. The width of each slot is also $d$. Except for the leftmost and rightmost slots, each slot is aligned with a gap between two nails in the bottom row. Let a small ball with diameter slightly smaller than $d$ roll down freely on the board, with its center initially aligned with the top nail. Each time the ball hits a nail, it may fall to the left or to the right (each with probability $1/2$), and the ball’s center will then align with the next nail it is going to hit. For example, Figure 2 shows one possible path of the ball. We know that the probability that the ball lands in slot $i$ is $p_i = \frac{C_n^i}{2^n} = \frac{ n! }{ 2^n i! (n-i)! }$, where $i$ is the slot index, from left to right: $0, 1, ..., n$. Now the problem is to compute, after removing some nails, the probability $p_m$ that the ball lands in the slot with index $m$. Assume that the nails in the bottom row will not be removed. For example, Figure 3 shows one possible path after some nails have been removed.  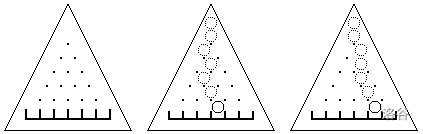Figure 1 $\qquad$ $\qquad$ $\quad$ $\quad$ Figure 2 $\quad$ $\qquad$ $\qquad$ $\quad$ Figure 3.

The first line contains integers $n$ ($2 \leq n \leq 50$) and $m$ ($0 \leq m \leq n$). The following $n$ lines give the nail information for the $n$ rows of nails on the board from top to bottom. In each line, `*` means the nail is still present, and `.` means the nail has been removed. Note that in these $n$ lines, spaces may appear anywhere.

Output only one line: an irreducible fraction ($0$ should be written as $0/1$), which is the probability $p_m$ that the ball lands in the slot with index $m$. Definition of an irreducible fraction: $A/B$ is an irreducible fraction if and only if $A$ and $B$ are positive integers and $A$ and $B$ have no common factor greater than $1$.

Translated by ChatGPT 5