P5752 [NOI1999] Chessboard Partition

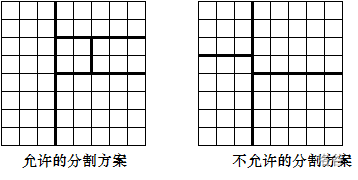
Partition an $8 \times 8$ chessboard as follows: cut off a rectangular piece from the original board such that the remaining part is also a rectangle, then continue partitioning the remaining part in the same way. After cutting $(n-1)$ times, together with the final remaining rectangle, there are a total of $n$ rectangular pieces. (Each cut can only be made along the edges of the grid cells.)  Each cell on the original board has a score. The total score of a rectangular piece is the sum of the scores of all cells it contains. Now you need to partition the board into $n$ rectangular pieces according to the rule above, and minimize the standard deviation of the total scores of all rectangular pieces. The standard deviation is $$\sigma = \sqrt{ \frac{ \sum_{i=1}^n (x_i - \bar x)^2 } { n }}$$ where the average is $$\bar x = \frac{\sum_{i=1}^n x_i}{n}$$ and $x_i$ is the score of the $i$-th rectangular piece. Given the board and $n$, compute the minimum possible value of $\sigma$.

The first line contains an integer $n$ ($1 < n < 15$). Lines 2 to 9 each contain $8$ non-negative integers less than $100$, representing the scores of the corresponding cells on the board. Adjacent numbers in each line are separated by one space.

Output only one number, $\sigma$, rounded to three digits after the decimal point.

Translated by ChatGPT 5