P5761 [NOI1997] Best Tour

There is a tourist city whose streets form a grid (as shown in the figure). The streets running west to east are “scenic roads”, with many sights along both sides. The streets running north to south are “tree-lined roads”, with no buildings on either side. Because there are many tourists, the “scenic roads” are designated as one-way streets: on a scenic road, tourists can only walk from west to east. On tree-lined roads, they can walk freely in any direction. A tourist is going to visit this city. Based on how much they like the sights, they assign a score to every scenic road segment. The score is an integer from $-100$ to $+100$. A larger score means the tourist likes the scenery on that scenic road segment more. Obviously, this tourist cannot give negative scores to all scenic road segments in the whole city.  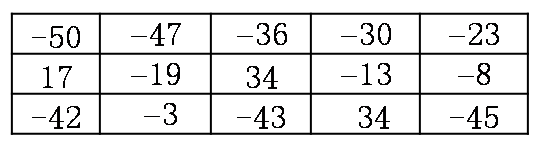The tourist may start the tour at any intersection and end at any intersection. They want the sum of the scores of all scenic road segments traveled along the way to be as large as possible. Please write a program to help the tourist find an optimal tour route.

The first line contains two integers $M$ and $N$, separated by a space. $M$ is the number of segments of the north-south tree-lined roads, and $N$ is the number of segments of the west-east scenic roads ($1 \le M \le 100$, $1 \le N \le 20001$). The next $M$ lines give the score information of the scenic roads from north to south. Each line contains $N - 1$ integers, describing the scores of each scenic road segment from west to east. Adjacent numbers in the same line are separated by a single space.

Only one line containing one integer, which is the total score of the optimal tour route found by your program.

**Explanation of the sample** The path is $17 \to -3 \to 34 \to 34$, and the answer is $82$. Translated by ChatGPT 5