P5781 [IOI 2019] Rectangular Regions

In the early 19th century, a ruler ordered a palace to be built on a plateau overlooking a beautiful river view. The plateau can be seen as an $n \times m$ grid made of square cells. The rows of the grid are numbered from $0$ to $n-1$, and the columns from $0$ to $m-1$. The cell in row $i$ and column $j$ ($0 \le i \le n-1$, $0 \le j \le m-1$) is denoted as cell $(i,j)$. Each cell $(i,j)$ has a specific elevation, denoted as $a_{i,j}$. The ruler instructed his architect to choose a rectangular region to build the palace. This region cannot include any cells on the boundary of the grid (row $0$, row $n-1$, column $0$, and column $m-1$). To do this, the architect should choose four integers $r_1$, $r_2$, $c_1$, and $c_2$ ($1 \le r_1 \le r_2 \le n-2$ and $1 \le c_1 \le c_2 \le m-2$), corresponding to the rectangular region that includes all cells $(i,j)$ satisfying $r_1 \le i \le r_2$ and $c_1 \le j \le c_2$. In addition, a region is considered valid if and only if, for every cell $(i,j)$ inside the region, the following condition holds: among the two cells adjacent to the region in row $i$ (cells $(i,c_1-1)$ and $(i,c_2+1)$), and the two cells adjacent to the region in column $j$ (cells $(r_1-1,j)$ and $(r_2+1,j)$), the elevation of cell $(i,j)$ must be strictly less than the elevations of all these four cells. Your task is to help the architect count the number of valid regions where the palace can be built (that is, the number of choices of $r_1$, $r_2$, $c_1$, and $c_2$ whose corresponding region is valid).

The first line contains two integers $n$ and $m$, representing the grid's height and width. The next $n$ lines each contain $m$ integers, which are $a_{i-1,0\dots m-1}$.

One line with one integer, representing the number of valid regions.

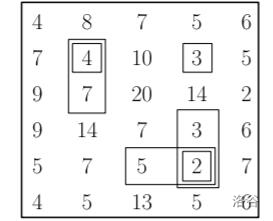
**Sample Explanation**  There are $6$ valid regions in total: - $r_1=r_2=1, c_1=c_2=1$ - $r_1=1, r_2=2, c_1=c_2=1$ - $r_1=r_2=1, c_1=c_2=3$ - $r_1=r_2=4, c_1=2,c_2=3$ - $r_1=r_2=4, c_1=c_2=3$ - $r_1=3,r_2=4,c_1=c_2=3$ For example, $r_1=1, r_2=2, c_1=c_2=1$ corresponds to a valid region because both of the following conditions hold: - $a_{1,1}=4$ is strictly less than $a_{0,1}=8$, $a_{3,1}=14$, $a_{1,0}=7$, and $a_{1,2}=10$. - $a_{2,1}=7$ is strictly less than $a_{0,1}=8$, $a_{3,1}=14$, $a_{2,0}=9$, and $a_{2,2}=20$. **Constraints** For all testdata: - $1 \le n, m \le 2500$. - $0 \le a_{i,j} \le 7 \times 10^6 (0 \le i \le n - 1, 0 \le j \le m - 1)$. The detailed additional constraints and scores for subtasks are shown in the table below: |Subtask ID|Additional Constraints|Score| |:-:|:-:|:-:| |$1$|$n, m \le 30$|$8$| |$2$|$n, m \le 80$|$7$| |$3$|$n, m \le 200$|$12$| |$4$|$n, m \le 700$|$22$| |$5$|$n \le 3$|$10$| |$6$|$0 \le a_{i,j} \le 1$|$13$| |$7$|No additional constraints|$28$| Translated by ChatGPT 5