P5786 [CQOI2008] Sensor Network.

A wireless sensor network consists of several devices that collect data independently and a control center. Each device must send the collected data to the control center for processing, but due to device limitations, not every device can connect directly to the control center. To solve this, you design the sensor network as a tree structure. The root of the tree is the control center, and each device has exactly one parent node (either the control center or another device). The number of child devices of a device is called its load level. The maximum load level among all devices (note that the control center is not a device) is called the network load level. Your task is to make the network load level as small as possible.

The first line contains an integer $N$, the number of devices. The second line contains $N$ characters, indicating whether each device can connect directly to the control center. The next $N$ lines each contain $N$ characters, where the $j$-th character in the $i$-th line is `Y` if and only if device $i$ can be a child of device $j$. If device $i$ can be a child of device $j$, then in any valid network, device $j$ will definitely not be a descendant of device $i$. In other words, if you treat these $N$ lines as the adjacency matrix of a directed graph, the graph has no directed cycles.

Output exactly one line containing $N$ integers, the parent of each device. Devices are numbered from $0$ to $N-1$ in input order, and the control center is denoted by $N$. If there are multiple solutions, output the lexicographically smallest one.

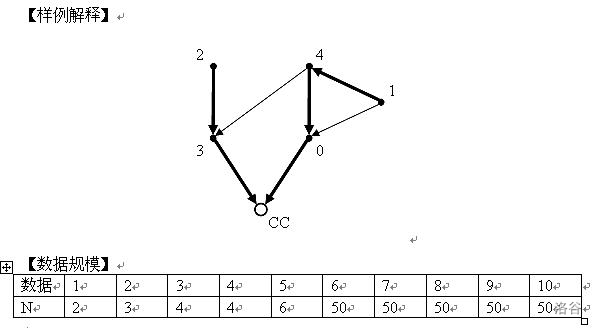
 For $50\%$ of the testdata, $2 \le N \le 6$; for the other $50\%$ of the testdata, $N = 50$. Constraints. Translated by ChatGPT 5