P5792 [CTSC2005] The Lonely Shepherd Girl

In Dalarna, Sweden, there is a high mountain. On the mountain there is a small cabin, where a shepherd girl lives. Every morning, a melodious flute sound comes from the neighboring mountain, and the shepherd girl responds from inside the cabin with her singing. The top view of the cabin is a simple polygon with $n$ vertices. Each wall can reflect sound, but due to unavoidable energy loss, the sound can be reflected at most $k$ times ($k=0$ means sound cannot be reflected). The walls are very smooth, so the reflection follows the law that the angle of reflection equals the angle of incidence, as shown in Figure $1$. Corners cannot reflect sound, but every other part of a wall—even very close to a corner—can reflect sound.  One day, the shepherd girl asked herself: at which places in the cabin can her singing be heard? Assume all listeners sit inside the cabin with their backs against the walls. Then what is the total length of the walls that her singing can reach? 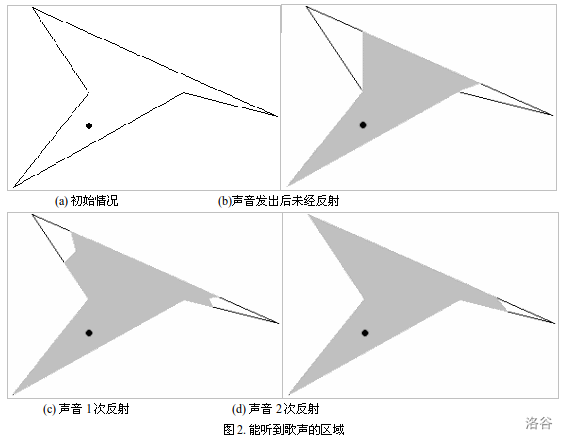The four diagrams in Figure $2$ show the initial situation and the regions reached after $0$, $1$, and $2$ reflections. The gray part indicates the area where the singing can be heard, and the black dot indicates the shepherd girl’s position. What you need to compute is the **total length** of the gray part on the polygon boundary. 

The first line contains $4$ integers $n, k, x, y$, representing the number of corners of the cabin, the maximum number of reflections, and the shepherd girl’s coordinates (her position is guaranteed to be inside the cabin and at least $1$ unit away from the walls). The next $n$ lines each contain two integers $x, y$, giving the coordinates of the $i$-th corner. The corners are listed in **clockwise or counterclockwise** order.

The output contains only one real number $L$, representing the total length of walls that can hear the singing. Print it with two decimal places.

#### Scoring A test point gets full score if the absolute difference between your output and the reference output is not greater than $0.02$. If the difference is greater than $0.02$ but not greater than $1$, then the test point gets $50\%$ of the score. In Sample $1$, answers $469.84$ and $469.88$ both get full score, while $468.86$ and $470.86$ both get $50\%$ of the score. #### Notes $3\leq n\leq 50$, $0\leq k\leq 5$, and all coordinates are integers with absolute value not exceeding $1000$. $50\%$ of the testdata satisfies $k\leq 1$. Translated by ChatGPT 5