P5796 [CQOI2006] 移动棋子

在一个 $n\times n$ 的棋盘上有 $n$ 枚棋子。每次可以把一枚棋子往上、下、左、右方向之一移动一格，最后排成一行、一列或者主、副对角线上（因此一共有 $2n+2$ 条可能的目标状态），要求移动次数最小。 棋盘上有一些位置是障碍，棋子在任何时候都不能经过。棋子的初始位置保证不在障碍物上。任两枚棋子不能在同时到达同一个格子。 　　　　　　

第一行包含两个整数 $n$，$m$，表示棋子的个数（它也是棋盘的边长）和障碍的个数。 以下 $n$ 行，每行两个整数 $x$ 和 $y$，表示第 $i$ 个棋子的坐标。（$1\le x,y\le n$） 以下 $m$ 行，每行给出一个障碍物的坐标。保证这 $n+m$ 个坐标两两不重合。

输出仅包含一个整数，表示最小移动步数。如果无解，输出`-1`。

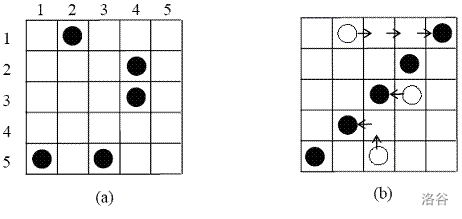
【样例解释】  【数据范围】 对于 $50\%$ 的数据，$n\le 15$，$m=0$； 对于 $100\%$ 的数据，$2\le n\le 50$，$0\le m\le 100$。