P5803 [SEERC 2019] Tree Permutations

有一天，Cool 先生建了一棵 $n$ 个点的树（没有环的无向连通图），他给任一编号 $i > 1$ 的点规定了两个值：$p_i < i$ 代表点 $i$ 的父节点，与 $w_i$ 代表 $i$ 与 $p_i$ 之间的边的边权。点 $1$ 是树根，所以它没有父节点。 你想知道 Cool 先生建的树长啥样，但是 Cool 先生拒绝告诉你，但他给了你一些提示： 他把所有的 $p_i$ 和 $w_i$ 值写成一列，得到了长为 $2 \cdot n - 2$ 的数列 $b$。 $$ b=[p_2, w_2, p_3, w_3, \dots, p_{n-1}, w_{n-1}, p_n, w_n] $$ 然后他将其随机打乱，得到了数列 $a$，并将 $a$ 告诉你。 然而只知道数列 $a$ 是无法还原那棵树的，你决定解决一个更难的问题。 定义一个树是 *$k$ 长*的，当且仅当点 $1$ 到点 $n$ 的路径上有恰好 $k$ 条边。 定义一个树是 *$k$ 完美*的，当且仅当这棵树是 *$k$ 长*的且点 $1$ 到点 $n$ 的路径上的边的边权之和是所有 *$k$ 长*的树中最大的。 你的任务是计算出每个 $k$ 值对应的 *$k$ 完美*的树中，点 $1$ 到点 $n$ 的路径上的边的边权之和。如果某个 $k$ 值不存在 *$k$ 完美*的树，则在该位置输出 $-1$。

第一行包含一个整数 $n \ (2 \leq n \leq 10^5)$，代表树上的节点数。 第二行包含 $2 \cdot n -2$ 个整数 $a_1, a_2, \dots, a_{2n-2} \ (1 \leq a_i \leq n-1)$，代表数列 $a$ 中的数字。

输出一行，共 $n-1$ 个空格隔开的整数 $w_1, w_2, w_3, \dots, w_{n-1}$，其中 $w_k$ 代表 *$k$ 完美*的树中点 $1$ 到点 $n$ 的路径上的边的边权之和。如果不存在 *$i$ 长*的树，则 $w_i=-1$。

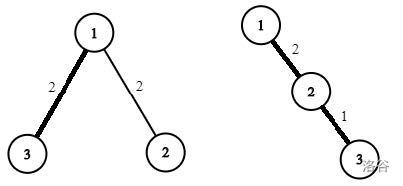
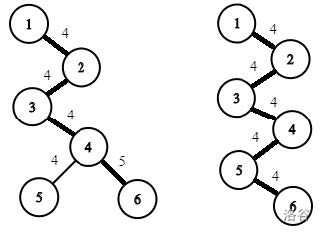
第一个样例中，*$1$ 完美*的树由数列 $[1, 2, 1, 2]$ 构成（即，$p_2=1, w_2=2, p_3=1, w_3=2$），*$2$ 完美*的树由数列 $[1, 2, 2, 1]$ 构成（即，$p_2=1, w_2=2, p_3=2, w_3=1$）。以下是这两棵树的图形（点 $1$ 到点 $n$ 的路径上的边都为粗线）。  第二个样例中，不存在能通过重排 $a$ 构造出的 *$k$ 完美*的树。 第三个样例中，只有 *$4$ 完美*的和 *$5$ 完美*的树可以被构造出。它们分别由数列 $[1, 4, 2, 4, 3, 4, 4, 4, 4, 5]$ 和 $[1, 4,2, 4, 3, 4, 4, 4, 5, 4]$ 构成。以下是这两棵树的图形。