P5803 [SEERC 2019] Tree Permutations

One day, Mr. Cool built a tree with $n$ vertices (a connected undirected graph with no cycles). For each vertex $i > 1$, he specified two values: $p_i < i$, which represents the parent of vertex $i$, and $w_i$, which represents the weight of the edge between $i$ and $p_i$. Vertex $1$ is the root of the tree, so it has no parent. You want to know what the tree Mr. Cool built looks like, but Mr. Cool refuses to tell you. However, he gave you some hints: He wrote all the values $p_i$ and $w_i$ into a single list, obtaining an array $b$ of length $2 \cdot n - 2$. $$ b=[p_2, w_2, p_3, w_3, \dots, p_{n-1}, w_{n-1}, p_n, w_n] $$ Then he randomly shuffled it, obtaining an array $a$, and told you $a$. However, knowing only the array $a$ is not enough to restore the tree, so you decide to solve a harder problem. A tree is called *$k$-long* if and only if the path from vertex $1$ to vertex $n$ contains exactly $k$ edges. A tree is called *$k$-perfect* if and only if it is *$k$-long*, and among all *$k$-long* trees, the sum of edge weights on the path from vertex $1$ to vertex $n$ is the maximum possible. Your task is to compute, for each $k$, the sum of edge weights on the path from vertex $1$ to vertex $n$ in a *$k$-perfect* tree. If no *$k$-perfect* tree exists for some $k$, output $-1$ at that position.

The first line contains an integer $n \ (2 \leq n \leq 10^5)$, representing the number of vertices in the tree. The second line contains $2 \cdot n -2$ integers $a_1, a_2, \dots, a_{2n-2} \ (1 \leq a_i \leq n-1)$, representing the elements of array $a$.

Output one line with $n-1$ space-separated integers $w_1, w_2, w_3, \dots, w_{n-1}$, where $w_k$ is the sum of edge weights on the path from vertex $1$ to vertex $n$ in a *$k$-perfect* tree. If no *$i$-long* tree exists, then $w_i=-1$.

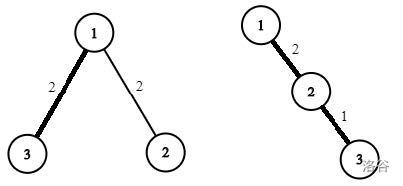
In the first sample, the *$1$-perfect* tree is formed by the list $[1, 2, 1, 2]$ (i.e., $p_2=1, w_2=2, p_3=1, w_3=2$), and the *$2$-perfect* tree is formed by the list $[1, 2, 2, 1]$ (i.e., $p_2=1, w_2=2, p_3=2, w_3=1$). The figures of these two trees are shown below (the edges on the path from vertex $1$ to vertex $n$ are drawn in bold).  In the second sample, there is no *$k$-perfect* tree that can be constructed by rearranging $a$. 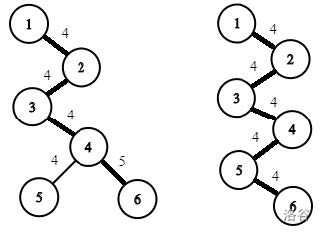In the third sample, only the *$4$-perfect* and *$5$-perfect* trees can be constructed. They are formed by the lists $[1, 4, 2, 4, 3, 4, 4, 4, 4, 5]$ and $[1, 4,2, 4, 3, 4, 4, 4, 5, 4]$, respectively. The figures of these two trees are shown below.  Translated by ChatGPT 5