P5811 [IOI 2019] Sightseeing Splitting

### Account bans for abusing this problem's judging. Note: This problem is judged in the traditional way, i.e., your program **must contain the `main` function**.

Baku has $n$ sightseeing spots, numbered from $0$ to $n-1$. There are also $m$ bidirectional roads, numbered from $0$ to $m-1$. Each road connects two different spots. Using these roads, it is possible to travel between any two spots. Fatima plans to visit all the spots within three days. She has decided to visit $a$ spots on the first day, $b$ spots on the second day, and $c$ spots on the third day. Therefore, she wants to split the $n$ spots into three sets $A$, $B$, and $C$, with sizes $a$, $b$, and $c$ respectively. Each spot belongs to exactly one set, so $a+b+c=n$. Fatima wants to find a split into $A$, $B$, and $C$ such that at least two of these three sets are connected. A set of spots $S$ is called connected if it is possible to travel between any two spots in $S$ using the roads, without having to pass through any spot not in $S$. If the above requirement is satisfied, then the split into $A$, $B$, and $C$ is called valid. Please help Fatima find a valid split (given $a$, $b$, and $c$), or determine that no valid split exists. If multiple valid splits exist, you may output any one of them. **Implementation details** You need to implement the following function: `int [] find_split（int n,int a,int b,int c,int [] p,int [] q）` - $n$: the number of sightseeing spots. - $a$, $b$, and $c$: the desired sizes of sets $A$, $B$, and $C$. - $p$ and $q$: arrays of length $m$ containing the endpoints of the roads. For each $i$ ($ 0 \le i \le m-1 $), $p[i]$ and $q[i]$ are the two spots connected by road $i$. - The function should return an array of length $n$. Call this array $s$. If no valid split exists, $s$ should contain $n$ zeros. Otherwise, for $0 \le i \le n-1$, $s[i]$ should be one of $1$, $2$, or $3$, indicating that spot $i$ is assigned to set $A$, $B$, or $C$, respectively.

The first line contains two positive integers $n$ and $m$. The second line contains three positive integers $a$, $b$, and $c$. Line $3+i$ (for $ 0 \le i \le m-1 $) contains two positive integers $p[i]$ and $q[i]$. Their meanings are the same as in the statement.

One line, containing the array returned by `find_split`.

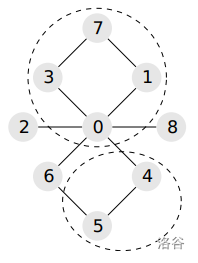
**Sample explanation**  One possible solution is $[1,1,3,1,2,2,3,1,3]$. This solution describes the following split: $A=\{0,1,3,7\}$, $B=\{4,5\}$, $C=\{2,6,8\}$. Sets $A$ and $B$ are connected. **Constraints** For $100\%$ of the testdata: - $3 \le n \le 10^5$. - $2 \le m \le 2 \times 10^5$. - $1 \le a,b,c \le n$. - $a+b+c=n$. - There is at most one road between each pair of spots. - Using these roads, it is possible to travel between any two spots. - For $0 \le i \le m-1$, $0 \le p[i],q[i] \le n-1$ and $p[i] ≠ q[i]$. **Subtasks** 1. ($7$ points) Each spot can be an endpoint of at most two roads. 2. ($11$ points) $a=1$. 3. ($22$ points) $m=n-1$. 4. ($24$ points) $n \le 2500$, $m \le 5000$. 5. ($36$ points) No additional constraints. Translated by ChatGPT 5