P5812 [IOI 2019] Skybridges

### Abuse of this problem’s judging system will result in account suspension. Note: This problem is judged in the traditional way, i.e., your program **must contain a `main` function**.

Kenan has drawn a plan of the buildings and skybridges along one side of Baku Avenue. The plan contains $n$ buildings, numbered from $0$ to $n-1$. It also contains $m$ skybridges, numbered from $0$ to $m-1$. The plan is drawn on a two-dimensional plane, where buildings and skybridges are vertical and horizontal line segments, respectively. The bottom of building $i$ ($0 \le i \le n-1$) is located at coordinate $(x[i],0)$, and its height is $h[i]$. Therefore, it corresponds to the line segment connecting $(x[i],0)$ and $(x[i],h[i])$. Skybridge $j$ ($0 \le j \le m-1$) has its two endpoints on building $l[j]$ and building $r[j]$, and has a positive $y$-coordinate $y[j]$. Therefore, it corresponds to the line segment connecting $(x[l[j]],y[j])$ and $(x[r[j]],y[j])$. A skybridge and a building are said to intersect if they share at least one common point. Thus, a skybridge intersects the two buildings at its endpoints, and it may also intersect other buildings in between. Kenan wants to find the length of the shortest path from the bottom of building $s$ to the bottom of building $g$, or determine that no such path exists. Pedestrians can only walk along buildings and skybridges, and are not allowed to walk on the ground, meaning they are not allowed to walk along the horizontal line with $y$-coordinate $0$. At any intersection point, a pedestrian can move from a skybridge onto a building, or from a building onto a skybridge. If an endpoint of one skybridge is at the same point as an endpoint of another skybridge, the pedestrian can also move from one skybridge to the other. Your task is to help Kenan answer his question. **Implementation Details** You need to implement the following function. `int64 min_distance(int[] x,int[] h,int[] l,int[] r,int[] y,int s,int g)` - $x$ and $h$: integer arrays of length $n$. - $l$, $r$, and $y$: integer arrays of length $m$. - $s$ and $g$: two integers. - If the shortest path from the bottom of building $s$ to the bottom of building $g$ exists, the function should return the length of the shortest path. Otherwise, it should return `-1`.

- Line $1$: $n$, $m$. - Line $2+i$ ($0 \le i \le n-1$): $x[i]$, $h[i]$. - Line $n+2+j$ ($0 \le j \le m-1$): $l[j]$, $r[j]$, $y[j]$. - Line $n+m+2$: $s$, $g$.

A single line containing the return value of the function `min_distance`.

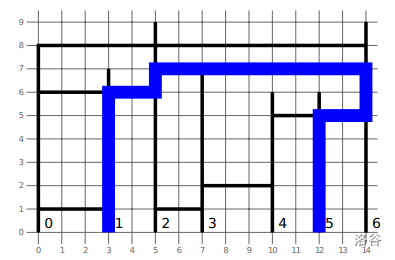
**Sample Explanation**  **Constraints** - $1 \le n,m \le 10^5$. - $0 \le x[0] < x[1] < \cdots < x[n-1] \le 10^9$. - $1 \le h[i] \le 10^9$ (for all $0 \le i \le n-1$). - $0 \le l[j] \le r[j] \le n-1$ (for all $0 \le j \le m-1$). - $1 \le y[j] \le \min(h[l[j]],h[r[j]])$ (for all $0 \le j \le m-1$). - $0 \le s,g \le n-1$. - $s \ne g$. - Except at endpoints, any two skybridges do not have any other common points. **Subtasks** 1. ($10$ points) $n,m \le 50$. 2. ($14$ points) Each skybridge intersects at most $10$ buildings. 3. ($15$ points) $s=0$, $g=n-1$, and all buildings have equal height. 4. ($18$ points) $s=0$, $g=n-1$. 5. ($43$ points) No additional constraints. Translated by ChatGPT 5