P5859 "SWTR-3" Plane Mirrors

Student $\mathrm{A}$ is studying physics. The teacher is explaining the physical phenomenon of “plane mirror imaging”. But the lecture is too boring, so he falls asleep.

Student $\mathrm{A}$ dreams that he is standing on a platform. Around him there are some plane mirrors, and we assume his position is $(0,0)$. He finds that each plane mirror has an initial opacity, denoted by $v_i$. In what follows, we define: - The “opacity” of a ray as: the sum of the initial opacities of all plane mirrors that the ray passes through. - The “visual opacity” of a plane mirror as: the maximum opacity among all rays that **originate from $(0,0)$** and **pass through that plane mirror**. Student $\mathrm{A}$ suddenly discovers that he can control these plane mirrors, so the following problem arises. Student $\mathrm{A}$ needs you to perform the following operations: `1 x1 y1 x2 y2 v`: Create a plane mirror whose two endpoints are at $(x_1,y_1),(x_2,y_2)$, with initial opacity $v$. `2 d`: Destroy the $d$-th created plane mirror. It is guaranteed that it has not been destroyed. `3 x y`: Let $\mathrm{A=(0,0),B=(x,y)}$. Query the opacity of the ray $\mathrm{AB}$. `4 d`: Query the visual opacity of the $d$-th plane mirror. If it has been destroyed, output `oops!`.

The first line contains an integer $n$, denoting the number of operations. The next $n$ lines: the $i$-th line starts with an integer $opt$, and then: - If $opt=1$, five integers $x_1,y_1,x_2,y_2,v$. - If $opt=3$, two integers $x,y$. - Otherwise, one integer $d$.

For each query of type $3$ or $4$, output one line with the answer.

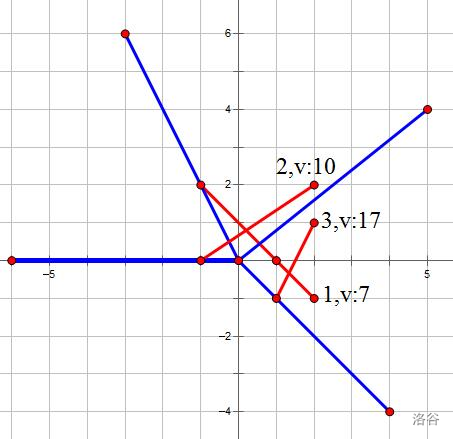
--- ### Sample Explanation  As shown in the figure, blue represents rays and red represents plane mirrors. For the 1st query: we can see the ray only passes through plane mirror $1$, so the answer is $7$. For the 2nd query: we can see the ray only passes through plane mirror $2$, so the answer is $10$. For the 3rd query: we can see the ray passes through plane mirrors $1,2$, so the answer is $7+10=17$. For the 4th query: we can see the ray passes through plane mirror $3$, so the answer is $17$. For the 5th query: we can see that among rays passing through plane mirror $2$, the ray with the maximum opacity is $(0,0)(2,2)$ (the ray is not unique). It passes through plane mirrors $1,2$, so the answer is $7+10=17$. For the 6th query: we can see that among rays passing through plane mirror $2$, the ray with the maximum opacity is $(0,0)(2,2)$ (the ray is not unique). It passes through plane mirror $2$, so the answer is $10$. For the 7th query: since plane mirror $1$ has been destroyed, output `oops!`. --- ### Constraints and Notes Test point ID|$n\leq$|Special property :-:|:-:|:-: $1-4$|$1000$|$|x|,|y|$ are less than $10^3$ and there are **no type $4$ queries** $5-8$|$2\times 10^5$|all $y$ are equal $9-12$|$2\times 10^5$|$x\ge 0$ $13-20$|$2\times 10^5$|none For $100\%$ of the testdata, $1\leq n\leq 2\times 10^5$, $1\leq v\leq 10^3$, and $0\leq |x|,|y|\leq 10^5$. It is guaranteed that the total number of plane mirrors will not exceed $10^5$. It is guaranteed that no plane mirror passes through $(0,0)$, but it is **not guaranteed** that a plane mirror will not degenerate into a point. It is guaranteed that for all type $3$ queries, $(x,y)\neq(0,0)$. --- For all test points, the time limit is $2\mathrm{s}$ and the memory limit is $128\mathrm{MB}$. Translated by ChatGPT 5