P5860 “SWTR-3” Counting Trees

On a sunny morning, Little $\mathrm{S}$ took his good friend Little $\mathrm{A}$ to count trees in a small forest. Looking at the forest full of trees, Little $\mathrm{S}$ suddenly got an idea and came up with a problem. --- $$\mathrm{Suddenly,\ Little\ S\ thought\ of\ a\ supercalifragilisticexpialidocious\ problem.}$$ $$\mathrm{He\ wanted\ Little\ A\ to\ answer\ it.}$$

There are $n$ vertices, and each vertex has a weight $v_i$. Little $\mathrm{S}$ wants Little $\mathrm{A}$ to choose some vertices to form a set. Let the set be $S=\{d_1,d_2,\dots,d_m\}(1\leq m\leq n)$. Of course, Little $\mathrm{A}$ also needs to ensure that these vertices can form a tree, and the degree of $d_i$ is $v_{d_i}(i\in[1,m])$. - Degree of a vertex: the number of vertices adjacent to it. Little $\mathrm{S}$ asks Little $\mathrm{A}$ how many ways there are that satisfy the conditions. Little $\mathrm{A}$ knows he definitely cannot solve this problem, so he asks you for help. Since the number of ways may be very large, output it modulo $998244353$.

The first line contains an integer $n$. The second line contains $n$ integers $v_1,v_2,\dots,v_n$.

Output one integer in one line, representing the number of valid ways.

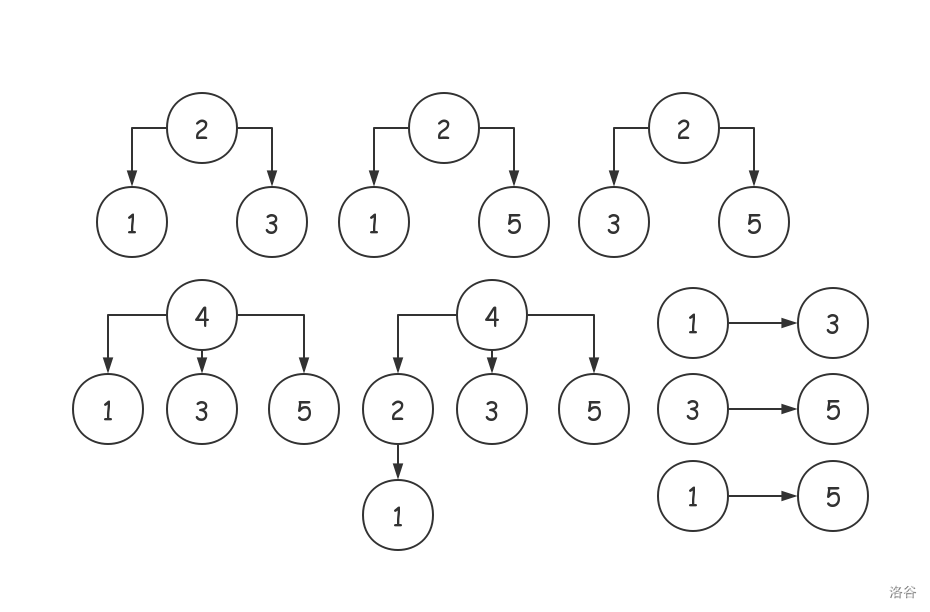
--- ### Sample Explanation - For sample $1$, it is enough to choose any two vertices among the three vertices. The answer is $C^{2}_{3}=3$. - For sample $2$, as shown in the figure, there are $8$ ways to choose vertices.  --- ### Constraints and Notes **This problem uses bundled testdata.** | Subtask ID | $n\leq$ | Special Property | Score | | :-: | :-: | :-: | :-: | | $1$ | $20$ | None | $11$ | | $2$ | $50$ | None | $12$ | | $3$ | $300$ | None | $10$ | | $4$ | $2500$ | None | $17$ | | $5$ | $4\times 10^4$ | None | $6$ | | $6$ | $3\times 10^5$ | $v_i\leq 3$ | $8$ | | $7$ | $3\times 10^5$ | Random testdata | $7$ | | $8$ | $5\times 10^5$ | None | $29$ | For $100\%$ of the testdata, $2 \leq n \leq 5 \times 10^5$ and $\ 1 \leq v_i \leq n$. --- In $\mathrm{Subtask\ 7}$, “random testdata” means: for every $v_i$, it equals $1$ with probability $\frac{1}{3}$, and with probability $\frac{2}{3}$ it is chosen uniformly at random from $[2,n]$. --- For the first $4$ $\mathrm{Subtask}$s, the time limit is $1\mathrm{s}$. For the $5$th $\mathrm{Subtask}$, the time limit is $3\mathrm{s}$. For the last $3$ $\mathrm{Subtask}$s, the time limit is $6\mathrm{s}$. For all test points, the memory limit is $256\mathrm{MB}$. Translated by ChatGPT 5