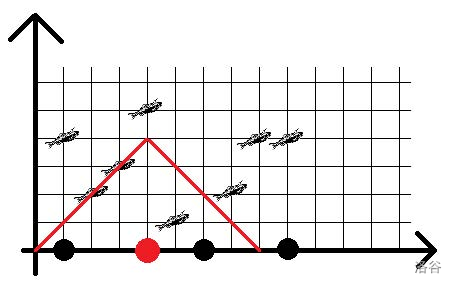
P5867 [SEERC 2018] Fishermen
题目描述
大海可以看成平面直角坐标系下的第一象限。海里有 $n$ 条鱼,每个鱼有一个二维坐标。一个点上可能有多条鱼。
海边有 $m$ 个渔夫,每个渔夫有一个 $x$ 坐标,而他们的 $y$ 坐标都是 $0$。
每个渔夫都有一根长为 $l$ 的钓竿,因此,他能钓到与他距离不超过 $l$ 的鱼。一个 $x$ 坐标为 $x$ 的渔夫和一条坐标为 $(a,b)$ 的鱼之间的距离为 $|a-x|+b$。
分别计算出对于每个渔夫,他可以钓到多少条鱼。
输入格式
第一行包含三个整数 $n, m$ 和 $l \ (1 \leq n,m \leq 2 \cdot 10^5, 1 \leq l \leq 10^9)$,代表鱼的数量、渔夫的数量和钓鱼竿的长度。
接下来 $n$ 行每行包含两个整数 $x_i$ 和 $y_i \ (1 \leq x_i, y_i \leq 10^9)$,代表每条鱼的坐标。
接下来一行包含 $m$ 个整数 $a_i \ (1 \leq a_i \leq 10^9)$,代表每个渔夫的 $x$ 坐标。
输出格式
对于每个渔夫,输出一行答案。
说明/提示
图片展示了上面的样例中第三个渔夫可以钓到鱼的区域。