P5867 [SEERC 2018] Fishermen

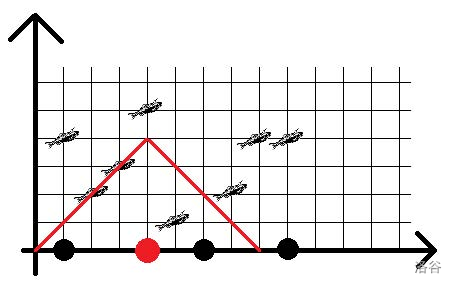
The sea can be considered as the first quadrant of the Cartesian coordinate system. There are $n$ fish in the sea, and each fish has a two-dimensional coordinate. There may be multiple fish at the same point. There are $m$ fishermen on the shore. Each fisherman has an $x$ coordinate, and their $y$ coordinate is always $0$. Each fisherman has a fishing rod of length $l$, so he can catch fish whose distance to him is at most $l$. The distance between a fisherman with $x$ coordinate $x$ and a fish at coordinate $(a,b)$ is $|a-x|+b$. For each fisherman, compute how many fish he can catch.

The first line contains three integers $n, m$ and $l \ (1 \leq n,m \leq 2 \cdot 10^5, 1 \leq l \leq 10^9)$, representing the number of fish, the number of fishermen, and the length of the fishing rod. The next $n$ lines each contain two integers $x_i$ and $y_i \ (1 \leq x_i, y_i \leq 10^9)$, representing the coordinates of each fish. The next line contains $m$ integers $a_i \ (1 \leq a_i \leq 10^9)$, representing the $x$ coordinate of each fisherman.

For each fisherman, output one line with the answer.

The picture shows the region where the third fisherman in the sample above can catch fish.  Translated by ChatGPT 5