P5869 [SEERC 2018] Matrix Queries

Given a $2^n \times 2^n$ matrix, initially every cell is white. Each cell can be either white or black. Define the *value* of a matrix as follows: 1. If the matrix is monochromatic, then its value is $1$ coin. 2. Otherwise, split the matrix into $4$ equal-sized submatrices. The value of the matrix is the sum of the values of the submatrices plus $1$ coin. You are given $q$ queries. Each query provides a row/column index $x$. You need to flip the color of every cell in that row/column (black becomes white, white becomes black), and then compute the *value* of the new matrix after the change.

The first line contains two integers $n$ and $q \ (0 \leq n \leq 20, 1 \leq q \leq 10^6)$, meaning the matrix size is $2^n \times 2^n$ and there are $q$ queries. The next $q$ lines each contain two integers $t$ and $x \ (0 \leq t \leq 1, 1 \leq x \leq 2^n)$. If $t=0$, flip the colors of row $x$; otherwise, flip the colors of column $x$.

For each query, output one line with the answer.

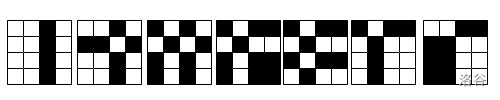
In the sample, the matrix after each query is shown in the figure below:  Translated by ChatGPT 5