P5895 [IOI 2013] dreaming Dreams

At the beginning of the world, IOI was still a distant dream. There are $N$ ponds where Serpent (the water snake) lives, numbered $0, \cdots, N - 1$, and there are $M$ undirected paths connecting these ponds. Between any two ponds, there is at most one route (a route consists of one or more paths) connecting them, and some ponds cannot reach each other at all (that is, $M \le N - 1$). It takes Serpent a fixed number of days to walk along each path, and different paths may take different numbers of days. Serpent's friend Kangaroo wants to build $N - M - 1$ new paths so that Serpent can travel between any two ponds. Kangaroo may build a path between any two ponds, and the time for Serpent to travel along each new path is always $L$ days. Kangaroo wants to find a way to build the paths such that, after building them, the maximum travel time between any two ponds is as small as possible. **Example**  In the figure above, there are $12$ ponds and $8$ paths ($N = 12, M = 8$). Suppose $L = 2$, meaning Serpent needs $2$ days to travel along any new path. Then Kangaroo can build $3$ new paths: - between pond $1$ and pond $2$; - between pond $1$ and pond $6$; - between pond $4$ and pond $10$.  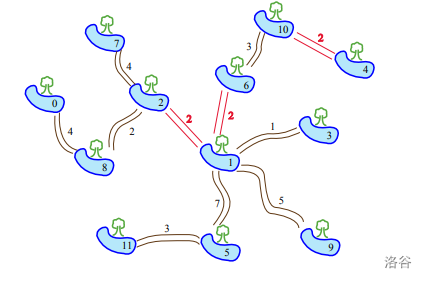The figure above shows the final state after building the paths. The longest travel time is from pond $0$ to pond $11$, which takes $18$ days. This is the best possible result: no matter how Kangaroo chooses to build the paths, there will always be some pair of ponds for which Serpent needs at least $18$ days to travel from one to the other.

- Line $1$: $N$ is the number of ponds, $M$ is the number of existing paths, and $L$ is the time for Serpent to travel along a newly built path. - Lines $2, \cdots, M + 1$: $A[i]$, $B[i]$, $T[i]$. $A$, $B$, and $T$ are three arrays of length $M$, representing the two endpoints of each path and the time to travel along it. For example, the $i$-th path connects pond $A[i-1]$ and pond $B[i-1]$, and it takes $T[i-1]$ days to travel along this path. For example, the sample in the statement should be written in the following format: ``` 12 8 2 0 8 4 8 2 2 2 7 4 5 11 3 5 1 7 1 3 1 1 9 5 10 6 3 ```

As described above, output the time required to travel between the two farthest ponds (i.e., the maximum travel time between any two ponds).

Constraints for $100\%$ of the data: $1 \le N \le 10^5$, $0 \le M \le N-1$, $0 \le A[i],B[i] \le N-1$, $1 \le T[i] \le 10^4$, $1 \le L \le 10^4$. Translated by ChatGPT 5